ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ. ТОЧКА НА ПРЯМОЙ.

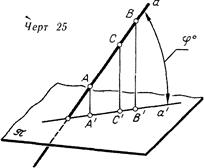
Чтобы получить проекцию прямой линии, достаточно спроецировать две ее точки, так как в общем случае проекцией прямой линии является прямая. Для доказательства этого возьмем на прямой а (черт. 25) две точки Л и 5 и спроецируем их на плоскость проекций л Их проекции А' и В' определяют пря­мую а', которую можно рассматривать как линию пересечения плоскости л с плоскостью, определяемой заданной прямой а и проецирующей прямой А—А'. Любая другая проецирующая прямая С—С', оче­видно, находится в этой плоскости и пересекается с плоскостью 'л в точке, лежа­щей на прямой а'. Таким образом, прямая а' является проекцией прямой а.

Если точка лежит на прямой линии, ее проекция находится на проекции этой прямой.

Из сравнения трапеций ABB'А' и ACC'A' (см. черт. 25) можно получить со­отношение: АВ : ВС==А'В':В'С; которое го­ворит о том, что проекция точки делит проек­цию отрезка прямой линии в таком отноше­нии, в каком точка делит заданный отрезок.

Из черт. 25 также очевидно, что проек­ция отрезка прямой меньше или, в частном случае, равна отрезку (А'В'=АВ cos <p°) Если прямая параллельна плоскости проекций (cos (p° = 1), отрезки ее проециру­ются равными им отрезками, если же перпендикулярна (cos (p°=0), проекцией прямой становится точка.

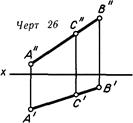
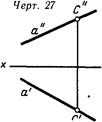
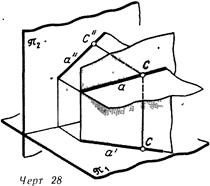
На эпюре прямую линию задают проекциями двух лежащих на ней точек (черт. 26) или прямыми линиями,.—ее проекциями (черт. 27), причем двух проек­ций — а' и а" достаточно для определения прямой а Чтобы убедиться в этом, обратим­ся к черт. 28, на котором видно, что каждая проекция прямой и проецирующие прямые (например, С—С' и С—С") опре­деляют две плоскости, которые пересекают­ся по линии, являющейся изображенной прямой а. На черт. 26 и 27 показана точка С, принадлежащая заданной прямой.

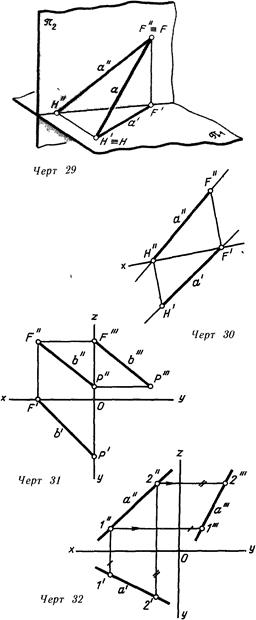
Точки, определяющие прямую, могут быть и точками общего положения (черт. 26) и точками, лежащими на плоскостях проекций (черт. 29, 30, 31). Во втором случае они называются следами пря­мой линии и являются точками пересе­чения ее с плоскостями проекций. Точка Н пересечения прямой с горизонтальной плос­костью проекций называется горизонталь­ным следом, а точка F пересечения с плоскостью V — фронтальным. Отрезок прямой а, ограниченный этими точками (черт. 30), находится в 1 четверти прост­ранства. Слева от точки Н прямая располо­жена в IV четверти, а справа от точки F — во II. Прямая Ь на черт. 31 определена фрон­тальным следом F и профильным Р.

Третью проекцию прямой (по двум за­данным) строят с помощью двух ее точек. На черт 32 профильная проекция прямой определена с помощью произвольно взятых точек / и 2. Через профильные проекции этих точек проведена линия а'"