ЧАСТНЫЕ ПОЛОЖЕНИЯ ПРЯМЫХ ЛИНИЙ

Прямые линии, изображенные на черт 26—32, называют прямыми общего положения Они не параллельны ни одной из плоскостей проекций

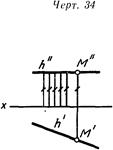
Линии частного положения параллельны одной или двум плоскостям проек­ций На черт 33 и 34 изображена горизонтальная линия h Высота, или уровень, всех ее точек одинакова, поэтому фронтальная ее проекция h" параллельна оси х, что является ее графическим признаком на эпюре. Такую линию называют горизонтальной линией уровня, или гори­зонталью.

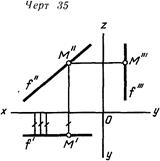
Прямая линия f, параллельная фронтальной плоскости проекций, называется фронтальной линией уровня* или ф р о н-талью (черт 35) Все точки ее одинаково удалены от плоскостиV поэтому горизон­тальная ее проекция f параллельна оси х

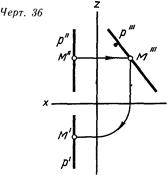
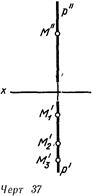
Прямая линия р, параллельная про­фильной плоскости проекций, называется профильной прямой Абсциссы ее точек одинаковы, поэтому горизонтальная и фронтальная ее проекции составляют одну прямую (черт 36) Обратим внимание на то, что в системе двух плоскостей проекций H/V линии h н f вполне опре­делены заданием их двух проекций, про­фильная же прямая может быть опреде­лена только заданием проекций двух ее точек Это легко увидеть, если попытаться задать на этих прямых какую-нибудь точку М ,На горизонтальной и фронтальной прямых точка М определяется однозначно (точке М" соответствует единственная точка М'), на профильной же линии р (черт 37) точкеM' может соответствовать на горизонтальной проекции и точка M'i, и точка М'-г, и любая другая точка линии р'

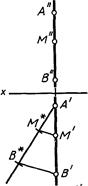
Все станет определенным, как только прямую р мы зададим двумя точками А и В (черт 38) Теперь фронтальная проекция М" точки М, взятой на прямой р (А, В), делит отрезок [А"—В"] в отношении А"М": М"В" В этом же отношении точка М делит отрезок [А—В] и точка М' — отрезок {{А'—Z']. Поэтому, для нахождения на чертеже горизонтальной проекции М' точки М отрезок [А'—В'] делят в отношении А"М": М"В" ( [А'—М*] = \А"—М"}, [М*—В*\ = [М"—В"], ЛГ—ЛГ || В'—В").

При наличии профильной проекции пря­мой р точку М' находят с помощью этой проекции (см. черт. 36).

Черт. 38

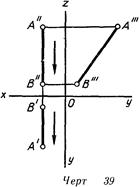
Особое положение профильных пря­мых линий в системе плоскостей проекции Л2/Я| делает желательным разделение их на две.группы: «восходящие» (черт. 36, 38) и «нисходящие» (черт. 39) прямые. Как увидим далее, это будет полезно при ре­шении некоторых вопросов изображения поверхностей. Различие этих прямых на эпюре очевидно только при наличии их профильной проекции. В случае, если про­фильной проекции нет, это можно сделать по следующему признаку: при чтении обо­значений точек, определяющих прямую, сверху вниз будем получать у восходя­щей прямой одинаковый порядок букв (А"^В" и А'-^В' на черт. 38), а у нисхо­дящей — различный (Л"->В" и В'->А' на черт. 39).

Прямые линии; параллельные двум плоскостям проекций, перпендикулярны к третьей. Последнее дает повод называть такие прямые проецирующими.

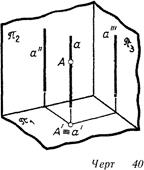
На черт 40 и 41 изображена гори­зонтально проецирующая прямая а. Она параллельна плоскостям V и W и перпендикулярна к горизонтальной плос­кости H). Такую прямую называют также вертикальной. Проекции а" и. а'" ее па­раллельны оси г, а горизонтальная проек­ция а' является точкой. (Проецирующая прямая может быть задана только одной точкой, являющейся ее изображением, с обязательным обозначением этой точки как проекции прямой линии).

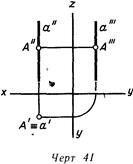
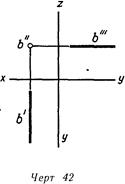
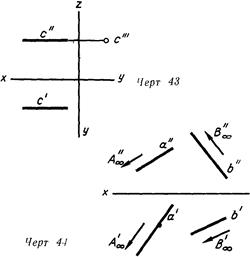
На черт. 42 дана фронтально проецирующая прямая Ь, а на черт. 43 — профильно проецирующая прямая с.

Любая точка, принадлежащая проеци­рующей прямой (черт. 40 и 41), проецируется на плоскость, перпендикуляр­ную к ней, точкой, совпадающей с проек­цией прямой (А'=а').

ПЛОСКОСТЬ