Объект регулирования и его статическая характеристика
Объект регулирования, например, двигатель, компрессор, котел и другие являются главным звеном системы автоматического регулирования, поэтому становится очевидным важность знания характеристик и свойств О. Как правило, О представляют в виде структурной схемы (см. рис. 5.9,а) с входными координатами подвода и отвода энергии и выходной координатой в виде регулируемого параметра. Соответственно выделяют канал регуляторной проводимости с коэффициентом статической передачи Кох и канал нагрузочной проводимости с коэффициентом статической передачи Коλ.
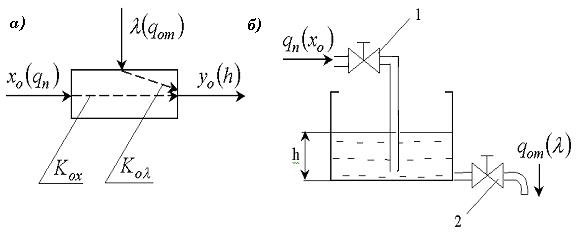
Рисунок 5.9. Структурная и функциональная схемы объекта
В данном случае в качестве объекта (рис. 5.9, а) выбрана емкость, в которую поступает жидкость через регулируемый вентиль 1 с текущим проходным сечением 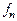 (подвод энергии
(подвод энергии 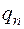 , где
, где 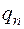 – расход жидкости), из емкости уходит определенное количество жидкости через вентиль 2 с проходным сечением
– расход жидкости), из емкости уходит определенное количество жидкости через вентиль 2 с проходным сечением 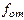 (отвод энергии
(отвод энергии 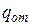 ). В зависимости от
). В зависимости от 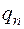 и
и 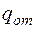 в емкости будет меняться уровень жидкости
в емкости будет меняться уровень жидкости 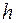 (регулируемый параметр или выходная координата объекта). Например, для судового двигателя под
(регулируемый параметр или выходная координата объекта). Например, для судового двигателя под 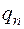 понимается эффективный крутящий момент на коленчатом вале, под
понимается эффективный крутящий момент на коленчатом вале, под 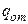 – момент сопротивления винта, а в зависимости от их соотношения установится значение частоты вращения (выходная координата
– момент сопротивления винта, а в зависимости от их соотношения установится значение частоты вращения (выходная координата 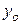 ).
).
Через первый канал осуществляется подвод энергии (подача топлива). Это канал регуляторной проводимости, именно по нему регулятор, изменяя подачу топлива, обеспечивает подвод энергии.
Отвод энергии (ее потребление) осуществляется винтом. Это канал нагрузочной проводимости, он обеспечивает отвод энергии.
Оба канала, как правило, работают независимо друг от друга. Поэтому возможно конечный эффект по изменению выходной координаты оценивать как сумму работы обоих каналов (принцип суперпозиции).
Таким образом,
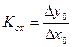 при
при 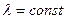
и 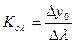 при
при 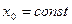 .
.
Рассмотрим подробнее работу объекта (рис. 5.9, б).
На базе уравнения Бернулли построим семейство расходных характеристик для gn при постоянном напоре с противодавлением h (здесь под gn имеем расход жидкости через вентиль с fn) – при фиксированном положении вентиля fот (рис. 5.10, а).

А б
Рисунок 5.10. Характеристики подвода и отвода энергии объекта
Перестроим графики исходя из того, что точки пересечения определяют равновесные режимы (рис. 5.11,а). Например, для рис. 5.10,а точка пересечения характеристики подвода энергии при 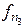 с характеристикой отвода энергии определится уравнением :
с характеристикой отвода энергии определится уравнением :
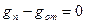
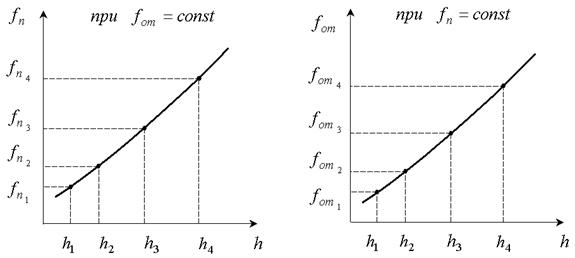 а б
а б
Рисунок 5.11. Статические характеристика каналов передачи объекта
Это выражение называется уравнением статики объекта, а регулируемый параметр определится как 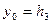 .
.
Запишем уравнение статики для канала регуляторной характеристики (рис. 5.11, а), предполагая линейность кривой, состоящей из равновесных точек
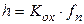 или
или 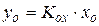 при
при 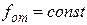 .
.
Аналогично представим уравнение статики для канала нагрузочной проводимости (рис. 5.11, б)
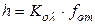 или
или 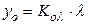 при
при 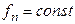 .
.
При совместной работе каналов, используя принцип суперпозиции, получим уравнение статики объекта
yo = Коλ ∙ λ + Кох ∙ хо .
Знаки членов правой части уравнения (1) определятся направленностью воздействия каждого канала на выходную координату. Тогда
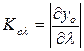 и
и  .
.
Например, для двигателя уравнение запишется как
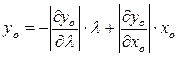 .
.
Таким образом, целесообразно введение понятия, определяющего поведение любого элемента САР, – статической характеристики. Статическая характеристика – это зависимость регулируемого параметра от входной координаты того или иного канала проводимости при фиксированном (выключенном) третьем канале проводимости, определенная во всем диапазоне регулирования. Например, для регулятора (см. рис. 1) это yp = f(xp) при
Для оценки устойчивости объекта и регулятора в статике вводится параметр фактор устойчивости, обозначаемый буквой F с соответствующим индексом (рис. 5.12).
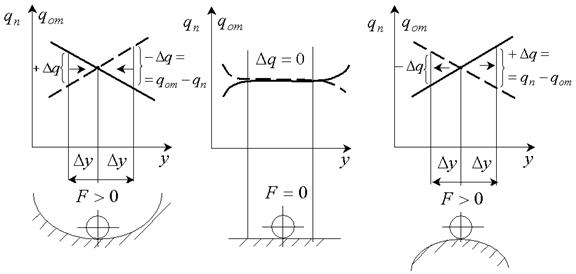
А б в
Рисунок 5.12. Геометрическая интерпретация устойчивости элемента САР
Пересечение кривых 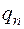 и
и 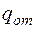 в соответствии с уравнением статики определит равновесный режим. При внесении возмущения
в соответствии с уравнением статики определит равновесный режим. При внесении возмущения 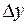 в ту или иную сторону в случае (рис. 5.12, а) приведет к нарушению баланса подвода и отвода энергии и соответствующему восстановлению исходного режима. Говорят, элемент обладает положительным самовыравниванием (фактор устойчивости
в ту или иную сторону в случае (рис. 5.12, а) приведет к нарушению баланса подвода и отвода энергии и соответствующему восстановлению исходного режима. Говорят, элемент обладает положительным самовыравниванием (фактор устойчивости 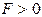 ). Положение шарика на выпуклой поверхности (геометрическая интерпретация ситуации, рис.5.12,в) неустойчиво. Фактор устойчивости
). Положение шарика на выпуклой поверхности (геометрическая интерпретация ситуации, рис.5.12,в) неустойчиво. Фактор устойчивости 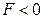 . Случай (рис. 5.12,б) определяет
. Случай (рис. 5.12,б) определяет 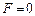 или безразличный режим, когда возмущение переводит шарик в другое положение.
или безразличный режим, когда возмущение переводит шарик в другое положение.
Предложено оценивать статическую устойчивость элемента САР соотношением
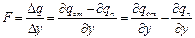 .
.
Так как
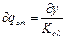 ,
, 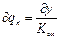 и Δg <0получим
и Δg <0получим
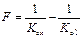 .
.
Дата добавления: 2019-09-30; просмотров: 827;











