Расчет электрохимической коррозии

Коррозионные потери металла пропорциональны величине коррозионного тока:

∆m=KI, (4.72)

где: ∆m – потери массы металла, K – коэффициент, I – величина коррозионного тока, связанная со скоростью коррозии уравнением (1.11).

Методы расчета коррозионного процесса делятся на аналитические и графические. При аналитическом расчете установившуюся величину коррозионного тока можно определить на основании закона Ома для гальванического элемента:

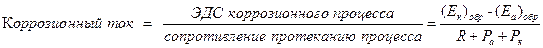, (4.72)

где [(E_k)_обр и (E_a)_обр – обратимые потенциалы катодного и анодного процессов соответственно; R – омическое сопротивление (электролита и металла) коррозионной системы; P_a и P_k – анодная и катодная поляризуемость соответственно (сопротивление протеканию коррозии, вызванного торможением анодного и катодного процесса).

Для большинства коррозионных систем омическое сопротивление невелико по сравнению с (P_a+P_k), т.е. R<< P_a+P_k. Поэтому максимальный коррозионный ток:

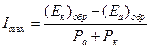(4.73)

Числитель уравнений (4.72) и (4.73) можно определить, рассчитав обратимые потенциалы, поляризуемости же анодного и катодного процессов в виде аналитической зависимости от тока P_a, P_k=f(I) можно приближенно оценить для простых случаев.

1) Для очень малых плотностей коррозионного тока, в области линейной зависимости:

Е_а = (Е_а)_обр +ΔЕ_а = (Е_а)_обр + к₁i_a, (4.74)

Е_k = (Е_k)_обр –ΔЕ_k = (Е_k)_обр – к₂i_k , (4.75)

R≈const, (4.76)

где: k₁ и k₂ – коэффициент пропорциональности.

Поскольку анодная и катодная плотности тока различны вследствие разных площадей анодных и катодных участков поверхности корродирующего металла:

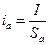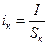, ; (4.77)

то 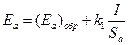, (4.78)

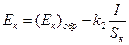, (4.79)

где: , .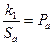

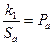Отсюда 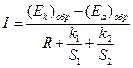(4.80)

2) При больших плотностях тока с логарифмической зависимостью поляризации от плотности тока (этот случай встречается чаще):

Е_a = (Е_a )_обр + ΔЕ_а = (Е_a )_обр + (а_а + b_а lni_а), (4.81)

Е_к = (Е_к )_обр - ΔЕ_к =(Е_к )_обр - (а_к + b_к lni_к ), (4.82)

R ≈ соnst.

При подстановке в уравнение (4.73) получается система уравнений, которые достаточно просто решаются графическими методами.

Пример 4.5. Элемент металлической конструкции состоит из участка поверхности цинка, в котором сделано отверстие и запрессована медная заклепка радиусом 8,03 мм. Рассчитать максимальную силу локального тока пара Сu-Zn в охлаждающем рассоле на основе водного 0,5н раствора NaCl при 293К если концентрация кислорода С 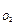= 2,25^.10^-7 г-моль/см³, коэффициент диффузии кислорода в данном растворе D 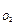=1,95^.10^-5 см²/с, толщина диффузионного слоя δ_d = 0,075 см. Сопоставить полученную величину с экспериментальным значением I = 52 мкА.

Решение. 1) В паре Сu-Zn медь является катодом, а цинк – анодом. Коррозионный ток локального элемента контролируется подводом кислорода к катоду.

Предельная катодная плотность тока равна: 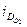= nFD ( 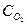)_o ( + ).

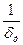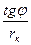2) Катодный ток I_к = i_к S_к = i 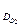·S_к = i 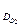^.πr 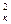= nFDC 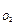^.πr_к( 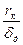+ tgφ)=

= 4 ^. 9600 ^. 2,25^.10^{-7 .}1,95 ^.10^{-5 .}3,14 ^. 0,803 ( 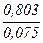+1,273) = 5,1^.10^-5 A= 51 мкА

3) Сравним полученное расчетное значение с экспериментальным: 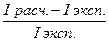^. 100 = 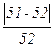^.100 ≈ 2 %.

Расчетное значение локального тока пары практически совпадает с измеренной величиной.