Обратимые потенциалы металлов, уравнение Нернста.
Исходя из предположения, что, если при взаимодействии металла с водным раствором электролита фазовую границу пересекают только ионы металла, то протекают два сопряженных процесса (А. Н. Фрумкин):
1) анодный (окислительный) процесс – переход ионов металла в раствор с образованием гидратированных ионов:
Ме + Н2О = Меn+·mH2O + ne, (4.5) скорость которого, измеряемая числом ионов, переходящих из твердой фазы в жидкую фазу в единицу времени, может быть выражена через плотность соответствующего тока прямого процесса 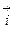 (рис. 4.4, а);
(рис. 4.4, а);
2) катодный (восстановительный) процесс – разряд гидратированных ионов из раствора с выделением их на поверхности металла в виде нейтральных атомов:
Меn+·mH2O + ne = Ме + Н2О, (4.6) скорость обратного процесса определяется соответствующей плотностью тока 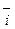 (катодный процесс практически используется для электрохимического осаждения гальванических покрытий).
(катодный процесс практически используется для электрохимического осаждения гальванических покрытий).
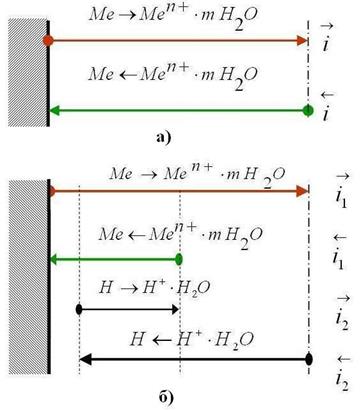
Рис. 4.4. Схема установления электродных потенциалов металлов:
а) – обратимого (равновесного), б) – необратимого.
Какой из этих процессов преобладает, определяется уровнем потенциальной энергии катионов в узлах кристаллической решетки металла ПMe и в растворе Пp. Если ПMe>Пр, то 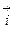 >
> 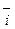 , то преобладает анодный процесс, суммарная скорость которого равна ia =
, то преобладает анодный процесс, суммарная скорость которого равна ia = 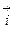 >
> 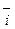 . Если Пр > ПМе, то
. Если Пр > ПМе, то 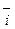 >
> 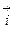 , то преобладает катодный процесс разряд ионов металла из раствора, суммарная скорость которого равна iк =
, то преобладает катодный процесс разряд ионов металла из раствора, суммарная скорость которого равна iк = 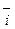 -
- 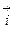 .
.
Образующийся ДЭС затрудняет протекание прямого процесса и облегчает протекание обратного. Когда потенциал в нем достигает значения, при котором энергетический уровень ионов в металле и растворе становится одинаковым, ПМе = Пр, устанавливается динамическое равновесие, при котором скорости анодного и катодного процессов равны:
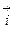 =
= 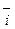 = i0, (4.7) где i0 – плотность тока обмена, обусловленная постоянно протекающим обменом ионами между металлом и раствором. (В водных растворах плотность тока обмена твердых металлов составляет 10-8 - 10-5 А/см2).
= i0, (4.7) где i0 – плотность тока обмена, обусловленная постоянно протекающим обменом ионами между металлом и раствором. (В водных растворах плотность тока обмена твердых металлов составляет 10-8 - 10-5 А/см2).
Этому равновесному состоянию соответствует некоторый скачок потенциала металла между металлом и раствором электролита, абсолютная величина которого неизвестна, поскольку разность потенциалов между двумя фазами нельзя измерить непосредственно. Для её определения измеряется э.д.с. элемента, составленного из исследуемого электрода (металла в электролите) и электрода сравнения. Эта э.д.с. и называется электродным потенциалом металла.
Обратимый (равновесный) электродный потенциал металла (ЕMe)o6p или ( 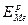 ) устанавливается, если в процессе обмена, определяющего потенциал металла в электролите, участвуют только ионы данного металла, т. е. когда металл находится в равновесии с собственными ионами в электролите (рис. 4.4, а).
) устанавливается, если в процессе обмена, определяющего потенциал металла в электролите, участвуют только ионы данного металла, т. е. когда металл находится в равновесии с собственными ионами в электролите (рис. 4.4, а).
В случае установления обратимого потенциала скорости анодного и катодного процессов равны ( 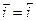 ), как и соответствующие заряды (количество электричества) процессов, и потерь массы металла нет (ΔmМе=0), т. е. коррозии (растворения) металла не происходит.
), как и соответствующие заряды (количество электричества) процессов, и потерь массы металла нет (ΔmМе=0), т. е. коррозии (растворения) металла не происходит.
Обратимый (равновесный) электродный потенциал металла рассчитывается по уравнению Нернста, его величина количественно характеризует способность металла посылать свои ионы в раствор электролита.
Уравнение Нернста может получено на основе термодинамических соотношений. Т.к. знак потенциала зависит от направления реакции, обратимо протекающие реакции записываются в восстановительной форме:
Меn+.mH2O+ ne 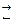 Ме + Н2О. (4.8)
Ме + Н2О. (4.8)
Для этой реакции уравнение изотермы Вант-Гофффа записывается как:
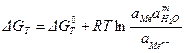 , (4.9) где
, (4.9) где 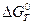 – стандартное изменение энергии Гиббса; R = 8,314 Дж/моль.К – универсальная газовая постоянная; T – температура, К; aMe ,
– стандартное изменение энергии Гиббса; R = 8,314 Дж/моль.К – универсальная газовая постоянная; T – температура, К; aMe , 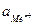 – активности металла и ионов металла в растворе.
– активности металла и ионов металла в растворе.
Поскольку, работа по созданию двойного электрического слоя (аналогично соотношению 4.2) равна убыли энергии Гиббса:
А= nFEдс= – ∆GТ, (4.10)
де Eдс – потенциал двойного электрического слоя (потенциал гальванического элемента металл-раствор или обратимый потенциал металла Еобр); n – заряд иона металла; F – постоянная Фарадея.
Подставляя (4.9) в уравнение 4.9, поскольку aMe =1, 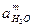 =1, получаем уравнение Нернста:
=1, получаем уравнение Нернста:
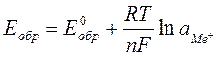 , (4.11)
, (4.11)
где 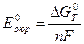 – стандартный обратимый потенциал металла (потенциал при Р=1атм =1,013·105 Па,
– стандартный обратимый потенциал металла (потенциал при Р=1атм =1,013·105 Па, 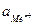 = 1 моль/кг).
= 1 моль/кг).
В общем случае, при протекании на поверхности металла, находящегося в контакте с электролитом, окислительно–восстановительной реакции с участием окисленной Ох и восстановленной Red форм вещества:
mOx + ke 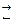 nRed, (4.12)
nRed, (4.12)
обратимый потенциал этой (катодной) реакции равен:
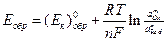 , (4.13)
, (4.13)
где 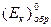 - стандартный окислительно-восстановительный потенциал реакции (обратимый или равновесный потенциал при
- стандартный окислительно-восстановительный потенциал реакции (обратимый или равновесный потенциал при 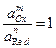 ),
), 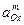 и
и 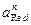 - активности окислителя и восстановителя с соответствующими стехиометрическими коэффициентами.
- активности окислителя и восстановителя с соответствующими стехиометрическими коэффициентами.
Стандартные потенциалы приведены в таблице 4.1.
Таблица 4.1.
Стандартные электродные потенциалы некоторых металлов и
окислительно-восстановительных реакций при 250С.
| Реакция | Потенциал, В | Реакция | Потенциал, В |
| Li++e=Li | –3,01 | H++ e = ½H2 | 0,000 |
| K++e=K | –2,925 | Sn4++4e=Sn | 0,007 |
| Na2++2e=Na | –2,900 | Cu2++2e=Cu | 0,337 |
| Mg2++2e=Mg | –2,370 | Cu++e=Cu | 0,521 |
| Al3++3e=Al | –1,660 | Fe3++e=Fe2+ | 0,77 |
| Ti2++2e=Ti | –1,630 | Ag++e=Ag | 0,799 |
| Ti3++3e=Ti | –1,210 | Hg2++2e=Hg | 0,854 |
| Mn2++2e=Mn | –1,180 | Pd2++2e=Pd | 0,987 |
| Cr2++2e=Cr | –0,913 | Ir3++3e=Ir | 1,150 |
| Zn2++2e=Zn | –0,762 | Pt2++2e=Pt | 1,190 |
| Cr3++3e=Cr | –0,740 | Au3++3e=Au | 1,500 |
| Fe2++2e=Fe | –0,440 | Au++e=Au | 1,690 |
| Cd2++2e=Cd | –0,402 | 2H2O+2e=H2+OH– (щелочные среды) | –0,828 |
| Mn3++3e=Mn | –0,283 | O2+2H2O+4e=4OH– (нейтральные и щелочные среды) | 0,401 |
| Ni2++2e=Ni | –0,250 | 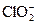 +H2O+2e=ClO–+2OH–
(щелочные среды) +H2O+2e=ClO–+2OH–
(щелочные среды)
| 0,66 |
| Mo3++3e=Mo | –0,200 | NO 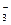 +4H++3e=NO+2H2O +4H++3e=NO+2H2O
| 0,96 |
| Sn2++2e=Sn | –0,136 | O2+4H++4e=2H2O (кислоты) | 1,23 |
| Pb2++2e=Pb | –0,126 | Cl2+2e=2Cl– | 1,36 |
| Fe3++3e=Fe | –0,037 | H2O2+2H++2e=2H2O | 1,78 |
Активность ионов в реакции диссоциации:
MmAn = mMZ+ + nAZ– (4.14)
определяется как произведение концентрации данного иона на средний коэффициент активности:
α+=С+ f± =Сm f± ; α–=С–·f± =Сn f±,(4.15)
где С+, С– – моляльные концентрации соответствующих ионов в растворе, m и n – число катионов и анионов, на которые распадается молекула при диссоциации, f± - средний ионный коэффициент активности.
Для труднорастворимых веществ, например гидрооксидов металлов:
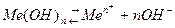 , (4.16)
, (4.16)
активность ионов металла:
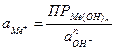 .
.
Пример 4.1. Рассчитать обратимый потенциал меди в 0,1 моляльном водном растворе СuSO4 при 298 К (средний ионный коэффициент активности ионов меди в данных условиях, 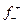 =0,15, берется по справочным данным).
=0,15, берется по справочным данным).
Решение. 1) Окислительно-восстановительная электродная реакция меди: Сu2++ 2е 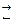 Сu.
Сu.
2) Обратимый потенциал меди находим по уравнению Hepнcтa: 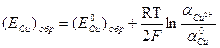 .
.
3) Активность ионов меди: 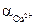 = с
= с 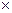 n
n 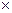
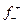 = =0,1
= =0,1 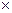 1
1 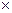 0,15 = 0,015, где: с – концентрация, n – количество ионов, переходящих в раствор. Активность твердых веществ всегда принимается равной единице:
0,15 = 0,015, где: с – концентрация, n – количество ионов, переходящих в раствор. Активность твердых веществ всегда принимается равной единице: 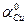 =1.
=1.
4) Стандартный обратимый потенциал для реакции берем из справочных данных (табл.4.1). Подставляем полученные данные и определяем: 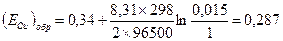 В.
В.
Пример 4.2. Найти обратимый потенциал кислородного электрода в нейтральном 1 m растворе Na2SO4 при 298 К в атмосфере воздуха.
Решение. 1) Кислород восстанавливается в катодном процессе по реакции: 2Н2О+О2+4е=4ОН 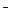 , обратимый потенциал которой по уравнению Нернста, с учетом данных по стандартному потенциалу реакции (табл.4.1)
, обратимый потенциал которой по уравнению Нернста, с учетом данных по стандартному потенциалу реакции (табл.4.1) 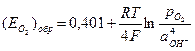 .
.
2) Активность газа определяется его парциальным давлением. Парциальное давление кислорода в воздухе 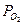 = 0,21 атм.
= 0,21 атм.
3) Активность гидрооксил-ионов в нейтральном растворе определяется через ионное произведение воды, КВ= 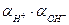 = 1,01 . 10-14 (для 298 К, значение берется по справочным данным). Отсюда
= 1,01 . 10-14 (для 298 К, значение берется по справочным данным). Отсюда 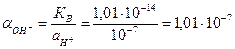 , поскольку рН=-lg
, поскольку рН=-lg 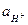 , и для нейтрального раствора равен 7.
, и для нейтрального раствора равен 7.
4) Подставляем полученные значения в уравнение Нернста: 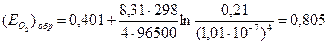 В.
В.
Дата добавления: 2017-02-13; просмотров: 5639;











