Ионно-электронная модель высокотемпературного окисления

Процесс роста оксидных пленок не ограничивается перемещением ионов по механизму диффузии вследствие градиента концентраций. Оксидные слои на металле являются ионными кристаллами, в кристаллической решетке которых под действием электрического поля происходит перемещение ионов и электронов с соответствующим типом проводимости, причем сумма чисел переноса катионов, анионов и электронов, t_к+t_а+t_э=1. Определяемые экспериментально соотношения чисел переноса позволяют определить преобладающий характер проводимости. Так, преимущественно катионная проводимость характерна для: AgCI, AgBr , АgJ , AgNО₃, NaCl и других щелочно-галоидных солей (<500 °С); анионная - PbF₂, РbС1₂, РbВг₂, BaF₃, ВаС1₂, ВаВг₂ (200-500°С); смешанная катионно-анионная - NaCI и другие щелочно-галоидные соли около температур плавления (>500°С), РbJ₂ (250°С); электронная проводимость характерна для металлов, Fe₃O₄, PbS; смешанная ионно-электронная проводимость - AgS, AgSe, NiO, FeS, смешанная ионно-электронная с преобладанием катионной - CuJ, Cu₂O, FeO, с преобладанием электронной проводимости – ZnO.

По ионно-электронной модели Вагнера рост оксидной пленки обусловлен работой гальванического элемента (рис.2.5): анод – поверхность металла на границе с пленкой, отдает катионы металла и электроны, катод – поверхность пленки на границе с окислителем, где ассимилируются электроны окислителем (кислородом) и образуются ионы О^2-. По этой схеме скорость процесса окисления определяется током гальванического элемента по законам Фарадея: 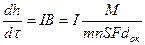, (2.29)

где I – величина тока, В – коэффициент перехода от массы к толщине пленки оксида М_mO_n, М и d_ок– молекулярная масса и плотность оксида, m – число атомов металла в оксиде, n – валентность металла, h – толщина пленки оксида площадью S, F –число Фарадея (96500 Кл/г-экв или 26,8 А^.ч/г-экв).

В таком концентрационном гальваническом элементе максимальная ЭДС обусловлена изменением энергии Гиббса в соответствии с уравнениями 2.2 и 2.7:

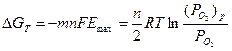, (2.30)

а общее сопротивление оксидной пленки R с удельной электропроводностью χ:

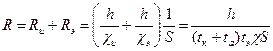, (2.31)

где R_и и R_э – ионное и электронное сопротивление; χ – общая удельная электропроводность пленки [Ом^-1см^-1] толщиной h [см] площадью S [см²]; χ_и = (t_к + t_а)^. χ – парциальная удельная электропроводность ионов; χ_э= t_э^. χ – парциальная удельная проводимость электронов в пленке; (t_к + t_а + t_э) =1 - числа переноса катионов, анионов и электронов.

На основе (2.30-2.31) и закона Ома (без учета поляризации) получаем уравнение: 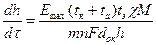, (2.32)

интегрируя которое, получаем параболическое уравнение для скорости роста пленки:

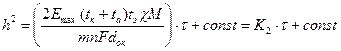, (2.33)

где К₂ – константа скорости окисления.

Ионно-электронная модель дает тот же параболический закон окисления, что и диффузионный механизм и позволяет рассчитать скорость газовой коррозии по известным физико-химическим свойствам образующихся продуктов. Из уравнения 2.33 следует, что К₂ увеличивается с ростом энергии Гиббса и ЭДС элемента Е_мах, при отсутствии химического сродства металла к кислороду (Е_мах=0), окисления не происходит. К₂ возрастает с увеличением удельной электропроводности пленки, χ, что совпадает с данными по скорости окисления металлов (табл. 2.1) и определяется соотношениями

Таблица 2.1

Удельная электропроводность оксидов [Ом^-1см^-1] при 727⁰К

между ионной и электронной проводимостями. Т.е. К₂ будет уменьшаться как при очень небольшой электронной проводимости, так и при отсутствии ионной проводимости. Максимальная скорость окисления наблюдается при t _э= t_к + t_а.