Основы теории подобия

Обработка методом теории подобия системы дифференциальных уравнений, которой описываются физические явления, позволяет получить следующий вид критериального уравнения:

Nu = f(Re, Gr, Pr, Fo), (6.2)

где 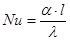– критерий Нуссельта, характеризующий конвективный теплообмен между жидкостью и поверхностью стенки; l – определяющий размер;

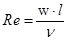– критерий Рейнольдса, характеризующий гидродинамический режим потока при вынужденном движении и является мерой соотношения сил инерции и вязкого трения;

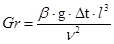– критерий Грасгофа, характеризующий соотношение сил вязкого трения и подъемной силы, описывает режим свободного движения теплоносителя, β – температурный коэффициент объемного расширения среды (для газов β=1/Т), g – ускорение свободного падения, ν – коэффициент кинематической вязкости;

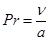– критерий Прандтля, характеризующий физическо-химические свойства жидкости, а – коэффициент температуропроводности.

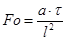– критерий Фурье, характеризующий нестационарный конвективный теплообмен, т.е. изменяющийся во времени, τ – время.

При решении конкретных задач уравнение (6.2) упрощается. Для установившегося движения жидкости выпадает критерий Фурье. При вынужденном турбулентном движении можно пренебречь влиянием свободного движения, выпадает критерий Грасгофа, и критериальное уравнение принимает вид:

Nu = f₁(Re, Pr), (6.3)

при чисто свободном движении жидкости выпадет критерий Re и появляется критерий Gr:

Nu = f₂(Gr, Pr). (6.4)

В случае рассмотрения в качестве среды газообразного теплоносителя, то исчезнет критерий Pr и уравнения (6.3), (6.4) примут вид: Nu = f₃(Re) и Nu = f₄(Gr), соответственно.