Основные свойства реального газа
Исследования свойств реальных газов показали, что их свойства отклоняются от законов, справедливых для идеальных газов. Отклонения возрастают с увеличением плотности. При условиях, близких к нормальным, аргон, водород, гелий наиболее, а диоксид углерода, кислород, азот и воздух наименее близки к свойствам идеального газа.
Молекулы реальных газов в отличии от идеальных имеют определенные (конечные) размеры, и между ними существуют силы межмолекулярного взаимодействия. При малых межмолекулярных расстояниях внутренние силы действуют как силы отталкивания, а при значительных расстояниях между молекулами действуют силы взаимного притяжения.
Уравнение состояния реального газа можно представить в форме:
рυ= zRT,(3.1)
где z – коэффициент сжимаемости, являющийся сложной функцией температуры и плотности (или давления), характеризует отклонение свойств реального газа от идеального.
Для идеального газа при любых параметрах z=1, а уравнение состояния – уравнение Клапейрона имеет вид:
рυ= RT (3.2)
Состояние реального газа описывает уравнение Ван-дер-Ваальса. Оно дает количественное представление о поведении газов, плотность которых не очень велика, и качественное представление о конденсации и критическом состоянии вещества. Большинство других существующих уравнений состояния применимы лишь в узком интервале переменных, либо имеют значительно более сложный вид. В связи с этим в инженерной практике широкое распространение получили различные таблицы и диаграммы.
В составе уравнения Ван-дер-Ваальса имеются две поправки, учитывающие отклонения реального газа от идеального.
Первая поправка учитывает объем молекул. Молекулы реального газа имеют определенные размеры. Если обозначить объем, занимаемый молекулами Vмол и зазорами между ними Vзаз, то свободный объем для движения молекул будет равен V-b, где b= Vмол+ Vзаз. Величина b – тот наименьший объем, до которого можно сжать газ.
Согласно уравнению Клапейрона давление идеального газа определяется как:
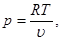 (3.3)
(3.3)
и для реального газа с учетом величины b:
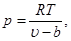 (3.4)
(3.4)
как видно из этих формул при одинаковой температуре давление в реальных газах будет больше.
Меньший свободный объем у реального газа в сравнении с идеальным приводит к большему числу соударений молекул реального газа о стенки, следовательно, к повышению давления.
Вторая поправка учитывает влияние сил взаимодействия между молекулами.
В идеальном газе молекулы движутся хаотично и удары о стенку сосуда ничем не ограничены, ввиду отсутствия сил взаимодействия между молекулами.
В реальном газе молекулы, находящиеся у стенок сосуда, притягиваются соседними молекулами внутрь сосуда. Количество ударов молекул о стенки сосуда, а значит и давление, будет меньше, чем в идеальном газе на величину ∆р, учитывающую силы взаимодействия между молекулами. Эта поправка ∆р прямо пропорциональна как числу притягиваемых, так и числу притягивающих молекул, или прямо пропорциональна квадрату его удельного объема:
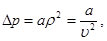 (3.5)
(3.5)
где 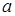 - коэффициент пропорциональности, принимающий для каждого газа определенное значение; ρ – плотность газа.
- коэффициент пропорциональности, принимающий для каждого газа определенное значение; ρ – плотность газа.
Уравнение Ван-дер-Ваальса принимает вид:
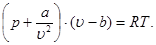 (3.6)
(3.6)
Уравнение качественно верно отображает поведение реальных веществ в жидком или газообразном состоянии. Для двухфазных состояний оно неприменимо.
Водяной пар
Водяной пар широко применяется в различных отраслях промышленности, главным образом, в качестве теплоносителя в теплообменных аппаратах и как рабочее тело в паросиловых установках.
Пары бывают насыщенные и перегретые. Насыщенные пары разделяют на сухие и влажные.
Для выяснения свойств пара и особенностей каждого из его состояний рассмотрим процесс превращения жидкости в пар, называемый иначе процессом парообразования. Известно, что жидкость может превращаться в пар при испарении и кипении.
Испарением называется парообразование, происходящее только с поверхности жидкости и при определенной температуре. Интенсивность испарения зависит от природы жидкости и ее температуры. Испарение жидкости может быть полным, если над жидкостью находится неограниченное пространство.
Явление испарения заключается в том, что отдельные молекулы жидкости, находящиеся у ее поверхности и обладающие высокими скоростями, а следовательно, и большей по сравнению с другими молекулами кинетической энергией, преодолевая силовое действие соседних молекул, вылетают из жидкости в окружающее пространство. С увеличением температуры интенсивность испарения возрастает, так как увеличиваются скорость и энергия молекул и уменьшаются силы их взаимодействия.
Массовая доля сухого пара во влажном паре называется степенью сухости или массовым паросодержанием и обозначается через х. Массовая доля жидкости во влажном паре называется степенью влажности и обозначается через у. Очевидно, что у = 1 - х. Степень сухости и степень влажности выражают или в долях единицы, или в %: например, если х = 0,95 и у = 1 - х = 0,05, то это означает, что в смеси находится 95% сухого пара и 5% кипящей жидкости.
Если температура пара выше температуры насыщенного пара того же давления, то такой пар называется перегретым. Разность между температурой перегретого пара и температурой насыщенного пара того же давления называется степенью перегрева.
Поскольку удельный объем перегретого пара больше удельного объема насыщенного пара (так как р = const, tпер > tн), то плотность перегретого пара меньше плотности насыщенного пара. Поэтому перегретый пар является ненасыщенным. По своим физическим свойствам перегретый пар приближается к газам и тем больше, чем выше степень его перегрева.
Среди диаграмм, характеризующих состояние водяного пара, наибольшее распространение получили Ts и is-диаграммы. Использование Ts–диаграммы позволяет легко определить количество тепла, участвующего в процессе, что обусловило ее применение для теоретического анализа экономичности тепловых двигателей. При расчетах различных процессов изменения состояния водяного пара используется главным образом is – диаграмма.
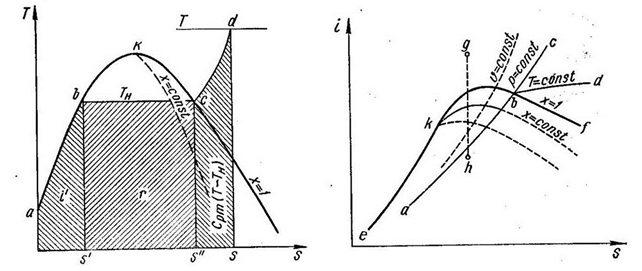
| Рис. 3.1. Тs – диаграмма для водяного пара | Рис. 3.2. is - диаграмма водяного пара |
На рис. 3.1 в координатах Ts изображен процесс парообразования при p=const (процесс abcd). Кривая аКс является пограничной кривой, аК – нижней пограничной кривой, Кс – верхней. Начало отсчета энтропии соответствует ее значению при температуре 273 К. Площадь под кривой процесса на Тs – диаграмме соответствует количеству теплоты.
Следовательно, площадь под изобарой ab эквивалентна энтальпии воды i' при температуре парообразования ТН. На изобарном участке bс, совпадающем с изотермой, происходит процесс парообразования, и площадь под прямой bс соответствует теплоте парообразования r. В изобарном процессе перегрева cd температура пара повышается до значения Т, и к пару подводится количество теплоты СР∙m∙(T-TН). Линии постоянной степени сухости х=const, как и на всех диаграммах, сходятся в критической точке К.
Точка встречи пограничных кривых называется критической точкой и обозначается буквой К. Эта точка соответствует некоторому предельному критическому состоянию вещества, когда отсутствует различие между жидкостью и паром. В этой точке отсутствует участок процесса парообразования. Параметры вещества при этом состоянии называются критическими. Например, для воды рк = 22,1145 МПа, Тк = 647,266 К; для диоксида углерода, рк = 7,32 МПа и Тк = 304,5 К и т. д.
Критическая температура является максимальной температурой насыщенного пара. При температуре выше критической могут находиться лишь перегретые пары и газы. Чем выше температура газа при данном давлении и чем ниже его критическая температура, тем ближе по своим свойствам он будет к идеальному газу.
На рис. 3.2 показаны различные процессы изменения состояния водяного пара на is–диаграмме. Область диаграммы, расположенная левее пограничной кривой еk, соответствует состоянию жидкости. Пограничная кривая kf делит диаграмму на две части. Выше этой кривой расположена область перегретого пара, а ниже – область влажного пара. На пограничной кривой kf пар является сухим насыщенным (х=1). Изобарный процесс изображен линией abc, изотермический – abd (в области влажного пара изотерма и изобара совпадают), изохорный – υ=const и адиабатный – gh. Кроме того, на этой диаграмме показаны линии постоянной степени сухости х=const.
Дата добавления: 2017-01-26; просмотров: 3921;











