Пример построения фазовых траекторий
Дано:
Уравнение состояния электрической печи сопротивления:
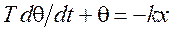 (3.3.)
(3.3.)
где q – колебание температуры, х - регулируемая величина.
Решение:
Статическую характеристику регулятора представим, как:
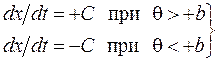 , при
, при 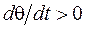
 , при
, при 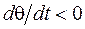 (3.4.)
(3.4.)
В данном случае + С – скорость вала исполняющего органа для уменьшения мощности, подводимой к печи; – С – скорость вала для увеличения подводимой мощности.
Продифференцируем уравнение (3.3.) и подставив значения dx/dt, получим уравнения, описывающие процесс системы регулирования температуры при разных положениях контактов реле:
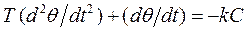 (3.5.)
(3.5.)
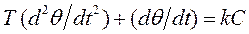 (3.6.)
(3.6.)
Построим фазовую траекторию в фазовой плоскости с координатами х = q и h = dq/dt. Согласно выражению (3.4.), если dq/dt > 0 контакты регулятора переключатся при q = +b (линия EF на рис.96,б), если dq/dt < 0, то регулятор переключится при q = –b (линия GH), как изображено на рисунке 96.
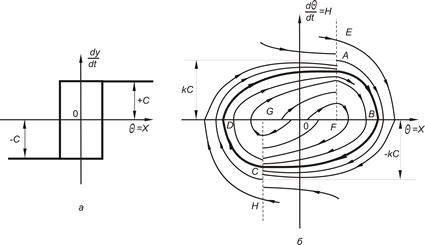
Рис.96. Графическое представление:
а) статической характеристики регулятора
б) фазового портрета системы регулирования температуры печи
Справа от ломаной EFGH на рисунке 96 фазовый портрет удовлетворяет условиям уравнения (3.5.), а слева от ломаной EFGH условиям уравнения (3.6.). Заменим в уравнении (3.5.) dt = dq/h и получим дифференциальное уравнение фазовых траекторий:
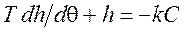 (3.7.)
(3.7.)
После интегрирования (3.7.) получим:
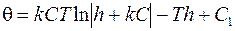 , (3.8.)
, (3.8.)
где C1 – постоянная интегрирования.
Подобным образом получим дифференциальное уравнение фазовых траекторий слева от ломаной EFGH, которое будет иметь вид:
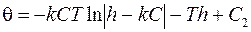 (3.9.)
(3.9.)
Кривые на фазовой плоскости, образующие фазовый портрет, представляют собой фазовые траектории при различных значениях С1 и С2, эти значения определяются начальными условиями. Вид фазового портрета характеризует переходной процесс в нелинейной системе. В нашем случае в системе характеризуется незатухающими колебаниями температуры, т.к. в фазовом портрете имеется замкнутый контур ABCD, выделенный жирной линией, к которому сходятся фазовые траектории.
Нелинейные системы могут характеризоваться установившимися состояниями равновесия, возникающими в них после окончания переходных процессов, и периодическими процессами, именуемыми автоколебаниями. Нелинейные системы могут иметь несколько состояний равновесия. Автоколебания возникают за счет свойств системы и не зависят от изменения внешнего воздействия. Линейные системы отличаются от нелинейных систем возможностью наличия у последних нескольких состояний равновесия и возможностью возникновения автоколебаний. В действительности рассматриваются только устойчивые состояния равновесия и автоколебания, причем устойчивость одних не исключает неустойчивости других.
От значения отклонения нелинейной системы от состояния равновесия может зависеть ее устойчивость, при этом различают устойчивость в «целом», в «большом» и в «малом». Устойчивость системы в «малом» характеризуется устойчивостью системы при малом отклонении от состояния равновесия. Устойчивость системы в «большом» говорит об устойчивости системы при большом отклонении. Система может быть устойчива в «малом» и неустойчива в «большом». Система считается устойчивой в «целом» при любых отклонениях.
Анализ фазовых портретов дает возможность охарактеризовать особенности устойчивости и возникновения автоколебаний. На рисунке 97,а представлен фазовый портрет системы, которая при любом начальном значении х придет в состояние равновесия (фазовые траектории приближаются к началу координат). О состоянии равновесия позволяет судить отрезок на оси абсцисс, к которому сходятся фазовые траектории, и размер которого зависит от величины области нечувствительности. Такая система считается устойчивой в «целом». На рис. 97,б изображен фазовый портрет системы, устойчивой в «малом» и неустойчивой в «большом». Данный вывод можно сделать на основании того, что при малых начальных значениях х фазовые траектории сходятся к началу координат, а при больших значениях х расходятся. Замкнутый контур фазовой траектории разграничивает устойчивость системы в «малом» от неустойчивости в «большом» и называется неустойчивым периодическим режимом или предельным циклом.
В данном случае наличие предельного цикла и направление фазовых траекторий от замкнутого контура указывает на невозможность возникновения устойчивых автоколебаний, т.к. колебания будут затухать или расходиться.

Рис.97. Фазовые портреты нелинейных систем управления:
а – система с областью нечувствительности (-b…+b), устойчивая в «целом»,
б – система, устойчивая в «малом» и неустойчивая в «большом»,
в – система с устойчивыми автоколебаниями,
г – система с двумя предельными циклами на фазовой плоскости.
На рисунке 97,в, на фазовом портрете видно наличие расходящегося до определенных значений процесса при малом отклонении системы от состояния равновесия. Имеет место неустойчивость системы в «малом», но при этом амплитуда колебаний увеличивается только до определенного значения, после которого остается постоянной, что говорит о возникновении устойчивых автоколебаний. Замкнутая фазовая траектория, к которой направлены другие фазовые траектории, говорит о наличии устойчивого предельного цикла. Следовательно, при любом значении х в системе возникнут автоколебания.
На рисунке 97,г фазовый портрет характеризует более сложную систему. На данном фазовом портрете изображены два замкнутых контура, указывающих на существование периодических режимов. Внутренний предельный контур неустойчив и является границей устойчивости в «малом». Внешний предельный контур устойчив и указывает на возможность возникновения устойчивых автоколебаний в системе.
Параметры автоколебаний определяются по замкнутому контуру. Например, при гармонических автоколебаниях, описываемых синусоидой х = А sin wt, амплитуду автоколебаний можно определить, как длину отрезка ОА на оси абсцисс на рисунке 97,в. На основании того, что х' = А cos wt, при cos wt = 1, отрезок ОВ равен Аw, поэтому частота автоколебаний w = ОВ /ОА.
В действительности причина появления автоколебаний объясняется заранее заданными переключениями в системе. В отличие от незатухающих колебаний автоколебания не характеризуются синусоидой, и их фазовая траектория не имеет форму эллипса, поэтому расчет сделан с допущениями.
* * *
С учетом вышесказанного сформулируем отличия устойчивости нелинейных систем от устойчивости линейных систем:
- устойчивая «в целом» нелинейная система может иметь несколько состояний равновесия, линейная система – одно;
- устойчивость линейных систем не зависит от величины начального отклонения от состояния равновесия или, тогда как устойчивость нелинейных систем – зависит;
- у нелинейных систем различают устойчивость в «целом», в «большом» и в «малом», у линейных систем подобная классификация отсутствует;
- у устойчивых нелинейных систем может существовать режим автоколебаний, у линейных систем – нет.
Дата добавления: 2017-01-26; просмотров: 3351;











