Начисление процентов в условиях инфляции

Следствия инфляции:

- падение покупательской способности денег (индекс ),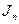

- рост цен (индекс роста цен 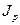=1/ ).

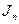Инфляцию необходимо учитывать, по крайней мере, в двух случаях:

1. При расчете наращенной суммы денег.

2. При измерении реальной эффективности (доходности) финансовой операции.

Пусть S – наращенная сумма денег без учета инфляции, С – наращенная сумма с учетом ее обесценения. Тогда

.

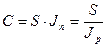Нетрудно связать индекс цен и темп инфляции. Под темпом инфляции h понимается относительный прирост цен за период. Обычно он измеряется в процентах и определяется как

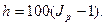
В свою очередь

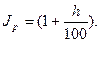
Например, если темп инфляции за период равен 30%, то это означает, что цены выросли в 1,3 раза.

Инфляция является цепным процессом. Следовательно, индекс роста цен за несколько периодов равен произведению цепных индексов цен:

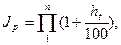
где 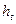– темп инфляции в периоде t.

Если h – постоянный ожидаемый (или прогнозируемый) темп инфляции за один период, то за n таких периодов получим

.

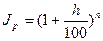Пример. (Экз. задача № 7) Вклад 25000 рублей положен в банк на полгода с ежемесячным начислением сложных процентов по номинальной ставке 32% годовых. Определить реальный доход вкладчика, если ожидаемый ежемесячный уровень инфляции составит 6%.

Решение.

n=1/2 года=6 мес.	1) наращенная сумма без учета инфляции:
P=25000 руб.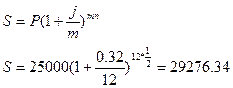
j=32 %
m=12 h=6%	2) наращенная сумма с учетом инфляции:
С-?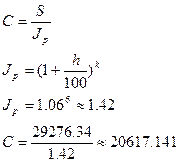

Формула Фишера – это формула, устанавливающая связь между темпом инфляции h, номинальной (без учета инфляции) i и реальной (с учетом инфляции) r ставками процента

.

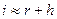Например, если субъект положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.

Темп инфляции за несколько периодов.Пусть темпы инфляции за последовательные периоды времени 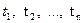равны 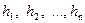соответственно. Тогда темп инфляции 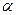за период 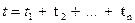приближенно равен:

.

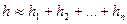Более точное выражение имеет вид:

.

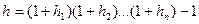Доказательства приведенных формул можно найти в учебном пособии П.Н. Брусов и др. «Финансовая математика», с. 31.