Производная функции в точке, ее геометрический и механический смысл
На рисунке изображены график функции
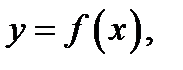 точки
точки 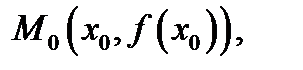
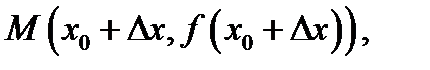
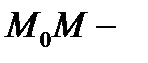 секущая,
секущая, 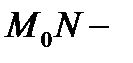 касательная к кривой
касательная к кривой 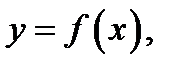 углы
углы 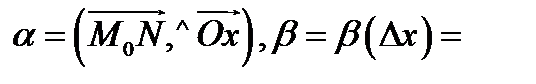
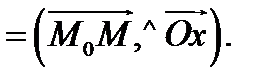 Пусть функция
Пусть функция 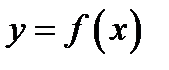 определена в точке
определена в точке 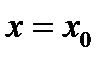 и некоторой ее окрестности
и некоторой ее окрестности 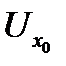 . Сместимся из точки
. Сместимся из точки 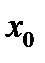 в точку
в точку 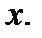 Величина
Величина 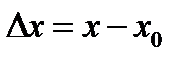 называется приращением аргумента в точке
называется приращением аргумента в точке 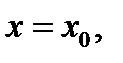 а величина
а величина 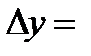 =
= 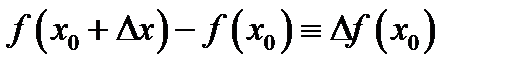 называется приращением функции
называется приращением функции 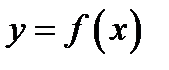 в точке
в точке  (соответствующим приращению
(соответствующим приращению 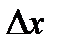 аргумента).
аргумента).
Определение 4. Если существует (конечный) предел
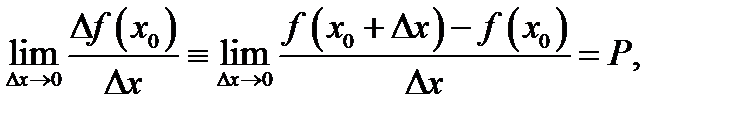
то его называют производной функции 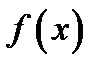 в точке
в точке  и обозначают
и обозначают 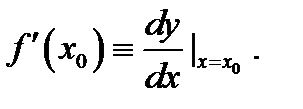 При этом функцию
При этом функцию 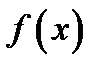 называют дифференцируемой в точке
называют дифференцируемой в точке 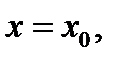 а
а
величину  называют дифференциалом функции
называют дифференциалом функции 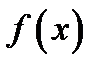 в точке
в точке 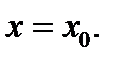
Выясним, в чем состоит геометрический смысл производной и дифференциала. Так как 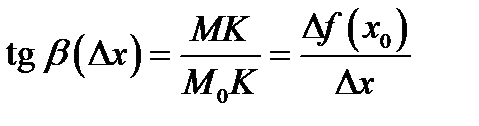 и так как
и так как 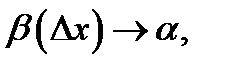 то
то 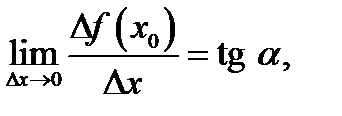 т.е.
т.е.
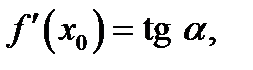 т.е. производная функции
т.е. производная функции 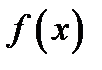 в точке
в точке  является угловым коэффициентом касательной к кривой
является угловым коэффициентом касательной к кривой 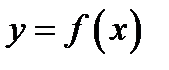 с точкой касания
с точкой касания 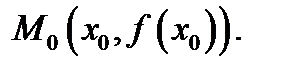
С другой стороны, из рисунка видно,что 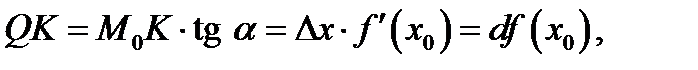 поэтому
поэтому
дифференциал 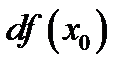 равен приращению касательной
равен приращению касательной 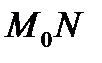 к графику функции
к графику функции 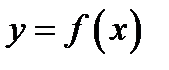 при переходе аргумента из точки
при переходе аргумента из точки 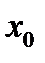 в точку
в точку 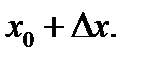
Из геометрического смысла производной легко получить уравнения касательной и нормали к кривой 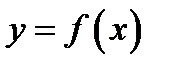 в точке
в точке 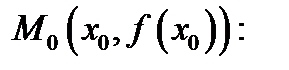
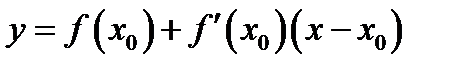 (касательная),
(касательная), 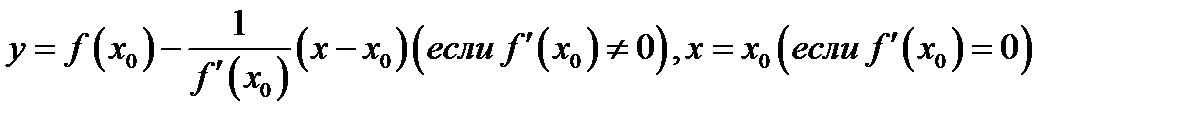 (нормаль).
(нормаль).
Выясним теперь механический смысл производной. Если 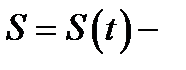 путь пройденный материальной точкой за время от момента
путь пройденный материальной точкой за время от момента 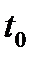 до момента
до момента 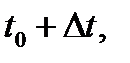 то
то 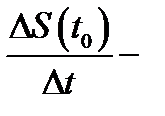 средняя скорость материальной точки, а величина
средняя скорость материальной точки, а величина
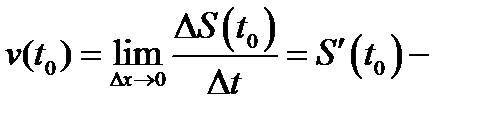 мгновенная скорость материальной точки в момент
мгновенная скорость материальной точки в момент 
Нетрудно показать, что
 любая дифференцируемая в точке
любая дифференцируемая в точке 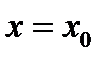 функция
функция 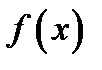 непрерывна в точке
непрерывна в точке 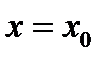 (обратное, вообще говоря, неверно; пример:
(обратное, вообще говоря, неверно; пример: 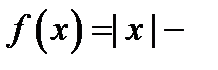 непрерывна в точке
непрерывна в точке 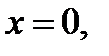 но
но 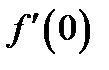 не существует).
не существует).
Дата добавления: 2016-06-05; просмотров: 1780;











