Бесконечно малые функции и их свойства
Понятие функции
Пусть даны два множества 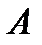 и
и 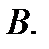
Определение 1.Говорят, что на множеситве 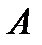 задана функция
задана функция 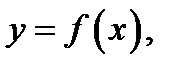 отображающая множество
отображающая множество 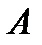 в множество
в множество 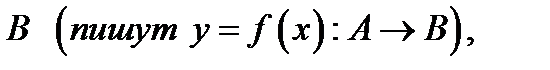 если каждому элементу
если каждому элементу 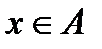 поставлен в соответствие единственный элемент
поставлен в соответствие единственный элемент 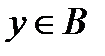 по закону
по закону 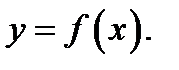 При этом
При этом 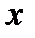 называется аргументом функции
называется аргументом функции 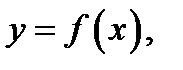 а
а 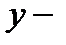 значением этой функции (при указаннном значении аргумента
значением этой функции (при указаннном значении аргумента 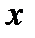 ). Множество
). Множество 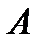 называется областью определения функции
называется областью определения функции 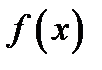 (обозначение:
(обозначение: 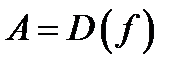 ), а множество
), а множество 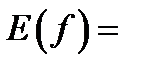
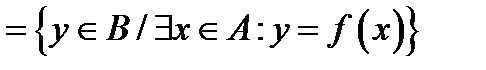 называется множеством значений этой функции.
называется множеством значений этой функции.
Чаще всего функцию задают двумя способами: а) табличный способ (здесь для каждого аргумента 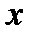 указывается соответствующий
указывается соответствующий 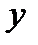 ) и б) аналитически (формулой; например
) и б) аналитически (формулой; например 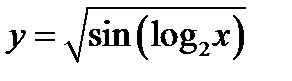 ). При аналитическом задании функции
). При аналитическом задании функции 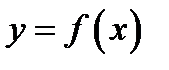 в качестве области определения обычно берут естественную область определения, т.е. множество
в качестве области определения обычно берут естественную область определения, т.е. множество 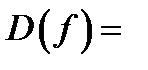 {
{ 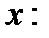 выражение
выражение 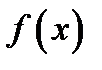 имеет смысл }. Например,
имеет смысл }. Например, 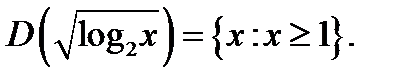 Будет также использоваться обозначение
Будет также использоваться обозначение 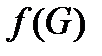 для множества всех значений
для множества всех значений 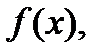 когда
когда 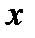 пробегает подмножество
пробегает подмножество 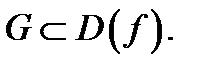
Предел функции
Сначала дадим понятие предела функции в конечной точке 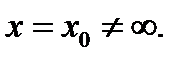 Различают проколотую
Различают проколотую 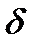 - окрестность
- окрестность 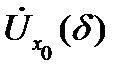 точки
точки 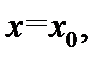 которая определяется как симметричный интервал
которая определяется как симметричный интервал 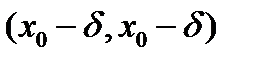 с выброшенной точкой
с выброшенной точкой 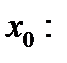
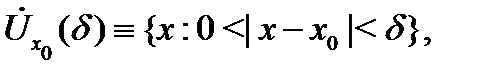
и просто 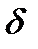 - окрестность
- окрестность 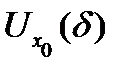 точки
точки 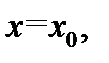 совпадающую с указанным интервалом:
совпадающую с указанным интервалом:
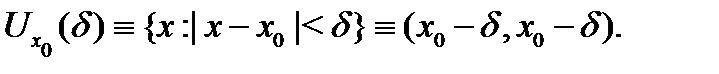
Пусть функция 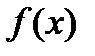 определена в некоторой проколотой окрестности
определена в некоторой проколотой окрестности 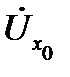 точки
точки 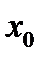 (в самой точке
(в самой точке 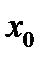 функция можеть быть определена или нет; её значение в точке
функция можеть быть определена или нет; её значение в точке 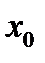 не существенно).
не существенно).
Определение 2. Говорят, что число P является пределом функции 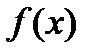 в точке
в точке 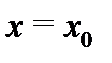 ( или при
( или при 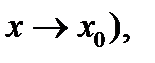 если для произвольного числа
если для произвольного числа 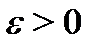 найдется число
найдется число 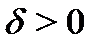 (зависящее, вообще говоря, от
(зависящее, вообще говоря, от 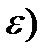 такое, что для всех значений
такое, что для всех значений 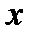 , удовлетворяющих неравенству
, удовлетворяющих неравенству 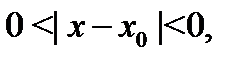 будет иметь место неравенство
будет иметь место неравенство 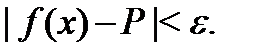 При этом пишут
При этом пишут 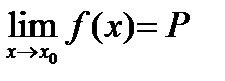 и читают: “ предел функции
и читают: “ предел функции 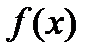 при
при 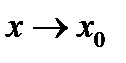 равен
равен 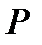 ”.
”.
Это определение записывают кратко так:
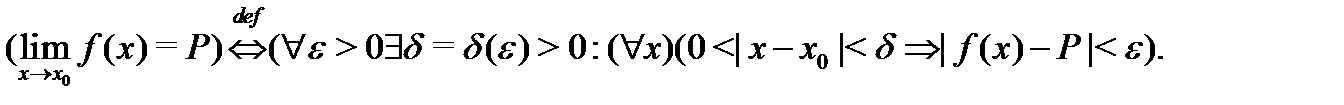
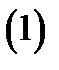
Отметим, что в этом определении не фигурирует значение функции 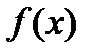 в точке
в точке 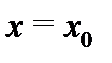 (
( 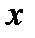 стремится к
стремится к 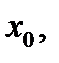 но
но 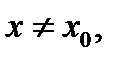 так как
так как 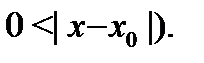 Это означает, что предел
Это означает, что предел 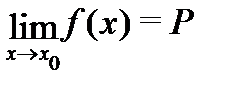 не зависит от того, каким является значение функции
не зависит от того, каким является значение функции 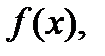 в точке
в точке 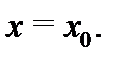 Например, функции
Например, функции
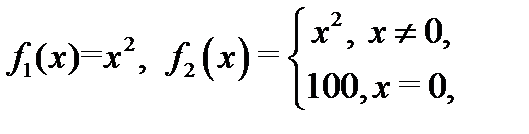
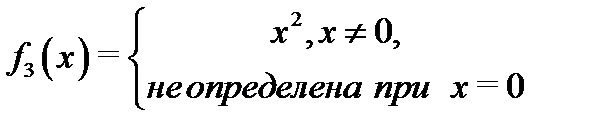
имеют один и тот же предел 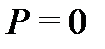 в точке
в точке 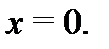
Геометрически высказывание (1) означает, что для любого 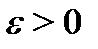 существует число
существует число 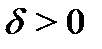 такое, что кривая
такое, что кривая 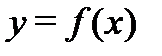 при всех
при всех 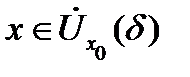 лежит внутри полосы
лежит внутри полосы 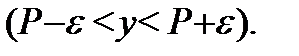 Если эта ситуация будет иметь место для произвольного интервала
Если эта ситуация будет иметь место для произвольного интервала 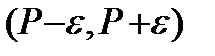 (или, что то же самое, для произвольного
(или, что то же самое, для произвольного 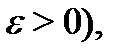 то число
то число 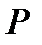 будет пределом функции
будет пределом функции 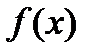 при
при  . Если же существует интервал
. Если же существует интервал 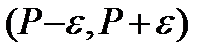 такой, что в любой проколотой окрестности
такой, что в любой проколотой окрестности 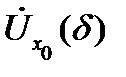 точки
точки 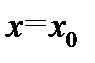 найдется абсцисса
найдется абсцисса 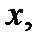 для которой
для которой 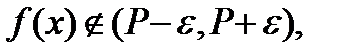 то
то 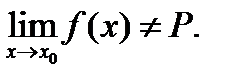 Геометрические соображения часто используют при доказательстве существования пределов для конкретных функций.
Геометрические соображения часто используют при доказательстве существования пределов для конкретных функций.
Теорема 1. Если существует (конечный) предел 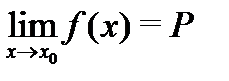 , то он единственен, а сама функция f(x) является ограниченной при
, то он единственен, а сама функция f(x) является ограниченной при 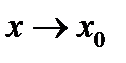 , т.е.
, т.е.
существуют постоянные 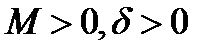 такие, что для всех
такие, что для всех 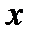 из проколотой окрестности
из проколотой окрестности 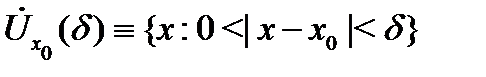 точки
точки 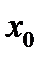 имеет место неравенство
имеет место неравенство 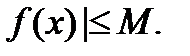
Замечание 1.Если функция 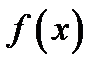 удовлетворяет условию, записанному в рамке,то ее называют функцией класса
удовлетворяет условию, записанному в рамке,то ее называют функцией класса 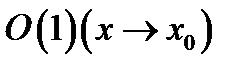 и пишут
и пишут 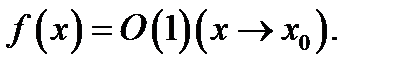 Функции класса
Функции класса 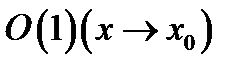 обладают следующими очевидными свойствами.
обладают следующими очевидными свойствами.
Теорема 2. Если 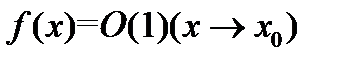 и
и 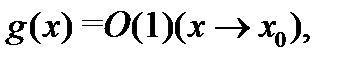 то
то
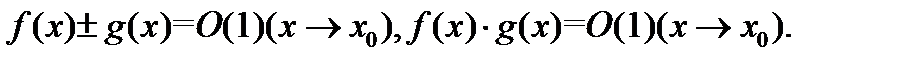
Бесконечно малые функции и их свойства
Определение 3. Функция 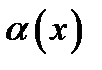 называется бесконечно малой функцией в точке
называется бесконечно малой функцией в точке 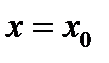 или функцией класса
или функцией класса 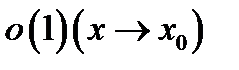 , если
, если 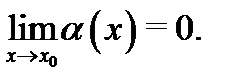 При этом пишут
При этом пишут 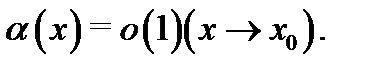 Таким образом,
Таким образом,
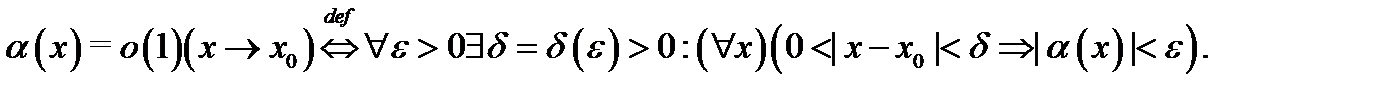
Например, функция 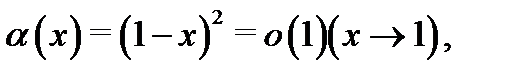 а функции
а функции 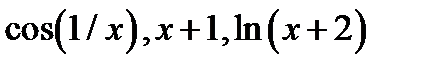 не являются функциями класса
не являются функциями класса 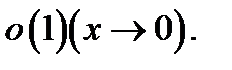
Теорема 3. Имеют место следующие свойства класса 
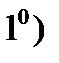 Если
Если  то
то 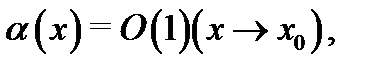 т.е.
т.е. 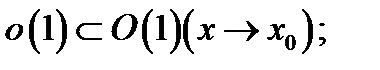
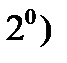
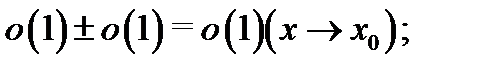
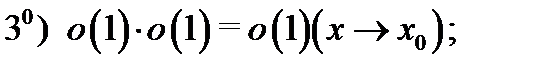
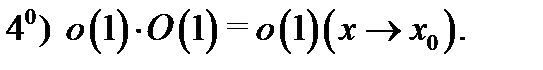
Доказательство. Свойство 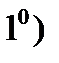 очевидно. Докажем свойство
очевидно. Докажем свойство 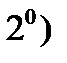 (другие свойства доказываются аналогично). Пусть
(другие свойства доказываются аналогично). Пусть 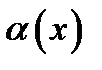 и
и 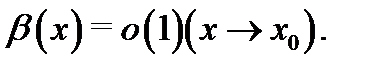 Тогда для произвольного
Тогда для произвольного 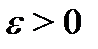 существуют числа
существуют числа 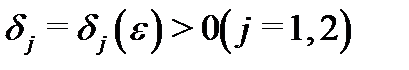 такие, что
такие, что
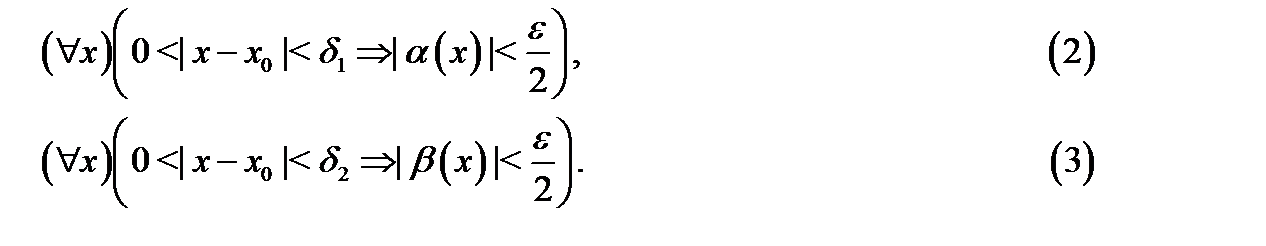
Выберем 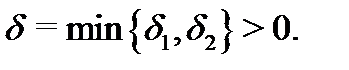 Тогда
Тогда 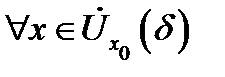 будут иметь место одновременно неравенства (2) и (3). Складывая их, получим, что
будут иметь место одновременно неравенства (2) и (3). Складывая их, получим, что
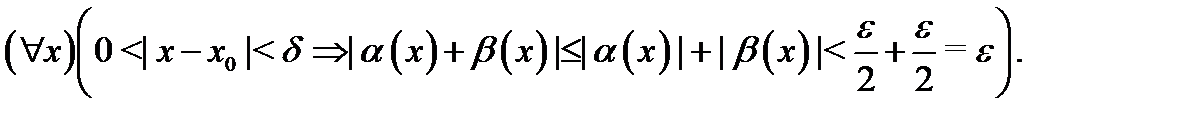
Это и означает, что 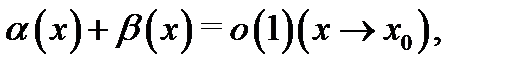 т.е. верно свойство
т.е. верно свойство 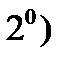 . Теорема доказана.
. Теорема доказана.
Следующая теорема устанавливает связь между бесконечно малыми функциями и функциями, имеющими предел при 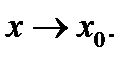
Теорема 4. Если существует (конечный) предел  то
то 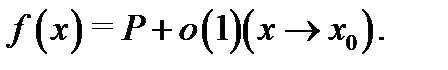 Обратно: если функция
Обратно: если функция 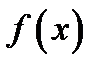 представляется в виде
представляется в виде 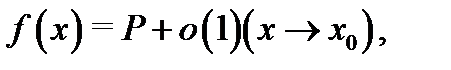 то
то 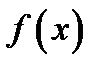 имеет предел в точке
имеет предел в точке  и
и 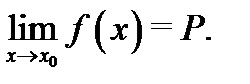
Доказательство. Существование предела 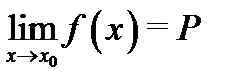 эквивалентно высказыванию
эквивалентно высказыванию
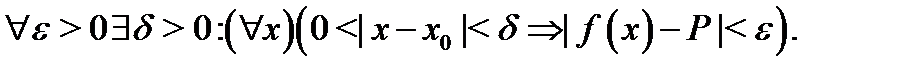
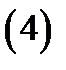
Высказывание (4), в свою очередь, эквивалентно тому, что функция 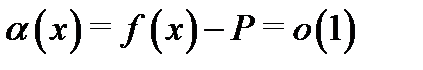
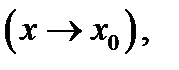 т. е. что
т. е. что 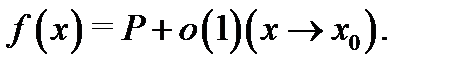 Теорема доказана.
Теорема доказана.
Замечание 2. Равенство 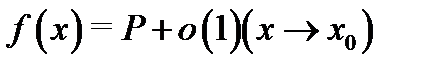 называют асимптотическим разложением функции
называют асимптотическим разложением функции 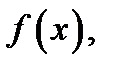 имеющей предел в точке
имеющей предел в точке 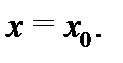
И, наконец, дадим определение предела функции в бесконечности. Сделаем это кратко.
Определение 4. Множества
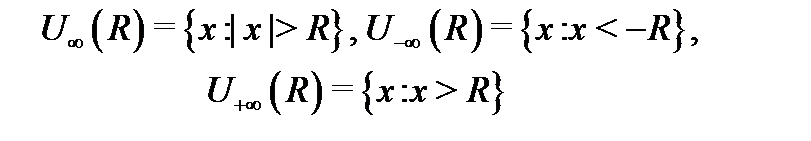
называются окрестностями точек 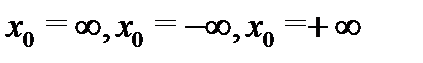 соответственно. Следующие высказывания являются определениями предела функции
соответственно. Следующие высказывания являются определениями предела функции 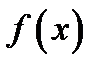 в бесконечности:
в бесконечности:
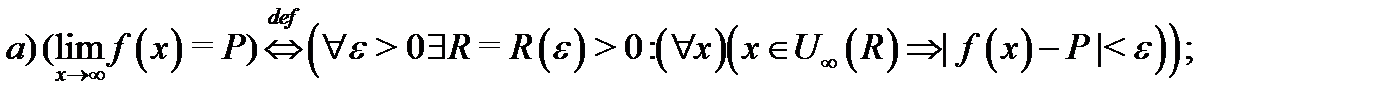
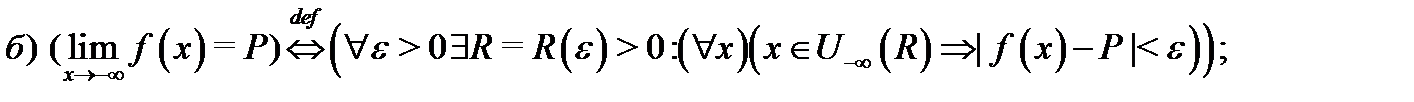
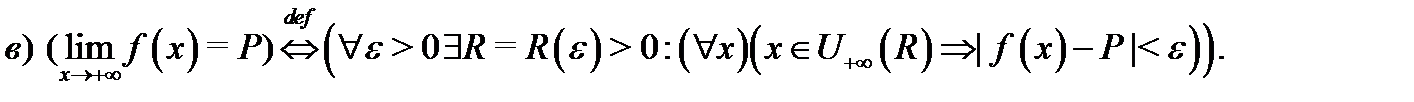
Перейдем теперь к обоснованию арифметических действий над пределами.
Теорема 5. Если существуют (конечные) пределы 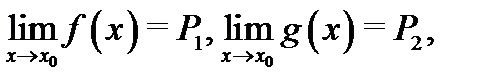 то и существуют пределы
то и существуют пределы 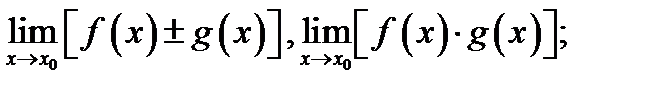 при этом
при этом
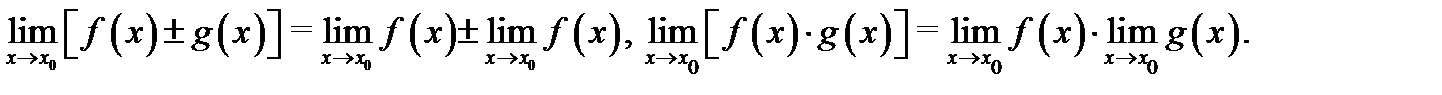
Если (кроме существования пределов 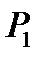 и
и 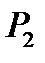 ) выполняется ещё условие
) выполняется ещё условие 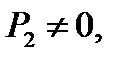 то существует предел
то существует предел 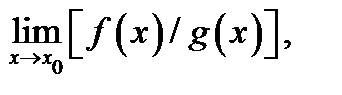 причем
причем
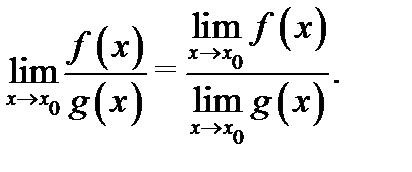
Доказательство. Докажем, например, теорему о пределе произведения. Так как существуют пределы 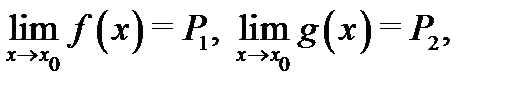 то по теореме 4 имеют место асимптотические разложения
то по теореме 4 имеют место асимптотические разложения  Умножая эти равенста друг на друга, будем иметь
Умножая эти равенста друг на друга, будем иметь 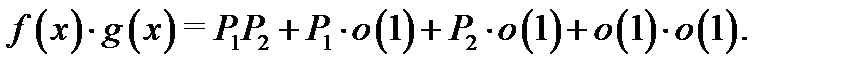 Поскольку
Поскольку 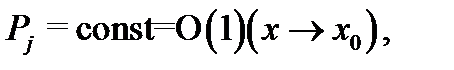 то
то 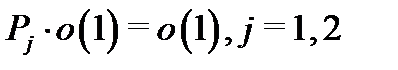 (см. теорему 3). Далее, поскольку
(см. теорему 3). Далее, поскольку 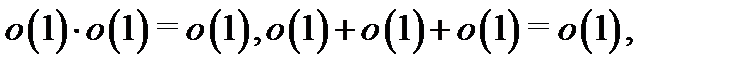 то функция
то функция 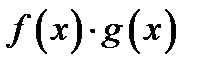 представляется в виде
представляется в виде 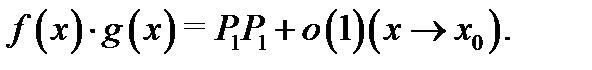 По теореме 14 отсюда следует, что существует предел произведения
По теореме 14 отсюда следует, что существует предел произведения 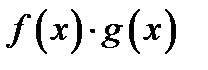 при
при 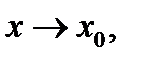 и он равен
и он равен
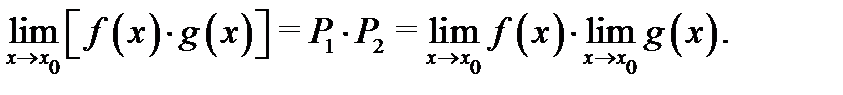
Теорема доказана.
6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых 
Введем следующее понятие. Пусть  конечная или бесконечная точка и пусть функ-
конечная или бесконечная точка и пусть функ-
ции 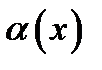 и
и 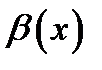 определены в некоторой проколотой окрестности точки
определены в некоторой проколотой окрестности точки 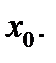
Определение 4.Две бесконечно малые функции 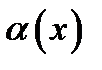 и
и 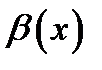 (при
(при 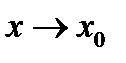 ) называются
) называются
эквивалентными, если 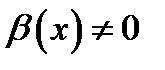 в некоторой проколотой окрестности
в некоторой проколотой окрестности 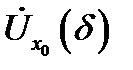 и если
и если
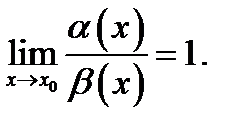
При этом пишут: 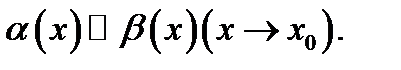
Важность этого понятия становится ясной при формулировке следующего утверждения.
Теорема 6. Если 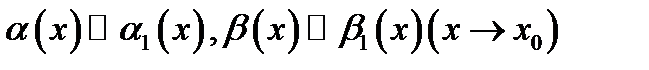 и если существует предел
и если существует предел 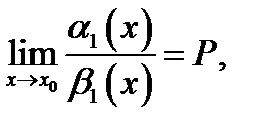 то существует и предел
то существует и предел 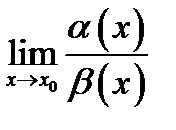 и он также равен числу
и он также равен числу 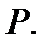
Доказательство.Переходя в тождестве 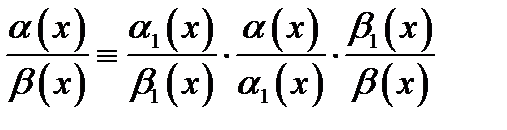 к пределу при
к пределу при 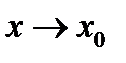 и учитывая, что
и учитывая, что 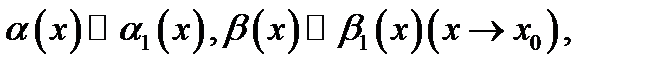 получаем утверждение теоремы.
получаем утверждение теоремы.
Используя эту теорему, а также таблицу эквивалентных бесконечно малых:
Таблица 1.
Если 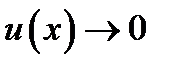 при
при 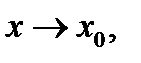 то при
то при 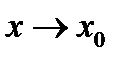 верны следующие соотношения:
верны следующие соотношения:
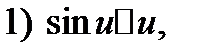
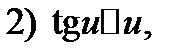
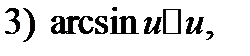
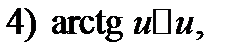
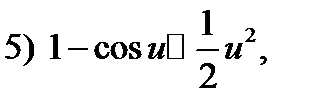
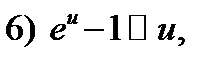
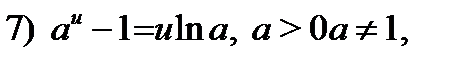
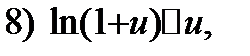
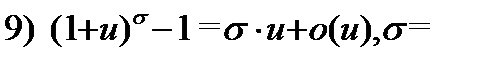 const.
const.
можно без особого труда вычислять пределы конкретных функций.
Пример 1. 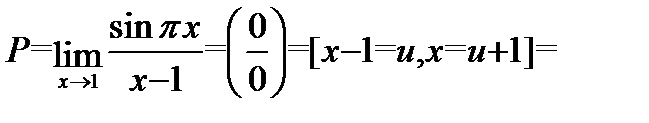
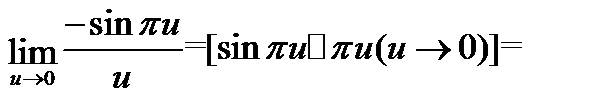
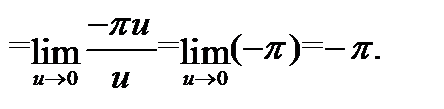
Дата добавления: 2016-06-05; просмотров: 2431;











