Наименьших квадратов
Конечная цель проведения эксперимента - установление функциональной связи (зависимости) между варьируемыми параметрами и выходным параметром и описание этой зависимости математической формулой.
Каждый эксперимент состоит из ряда опытов. В каждом опыте принимаются разные значения исследуемого параметра. Для обеспечения требуемой точности эксперимента в каждом опыте проводится определенное количество повторений или дублей. Например, для обеспечения уровня надежности (доверительной вероятности) 0,9 количество дублей в каждом опыте должно быть не менее 5. Для обеспечения уровня надежности (доверительной вероятности) 0,95 количество повторений должно быть не менее 7.
В основном для обработки экспериментальных данных с применением ЭВМ применяют метод наименьших квадратов (метод Гаусса).
Для понимания сути данного метода рассмотрим сначала рис.3.4. На нем в обычных и логарифмических координатах изображены опытные значения (точки) и, соответственно, аппроксимирующая кривая и аппроксимирующая прямая.

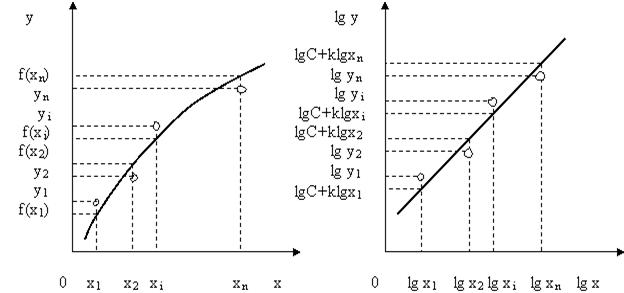
Рис.3.4. Иллюстрация реализации метода наименьших квадратов
На рис. 3.4 y1, y2, …, yn – экспериментальные значения, f(x1), f(x2), …, f(xn) – расчетные значения аппроксимирующей функции. Аналогичные значения, но только в логарифмическом измерении, приведены на правой части рисунка.
В основе метода наименьших квадратов лежит следующее положение: наилучшее приближение аппроксимирующей функции y = f(x) к экспериментальным данным будет в том случае, когда сумма квадратов отклонений расчетных значений f(x1), f(x2), …, f(xn) от экспериментальных данных y1, y2 … yn, является минимальной [16], т.е.
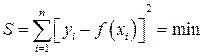
или
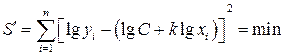 .
.
Разность 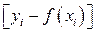 в выражении для S есть отклонение по ординате i – ой экспериментальной точки от заменяющей (аппроксимирующей) кривой. Квадраты отклонений берутся, чтобы компенсировать знаки «–» отклонений.
в выражении для S есть отклонение по ординате i – ой экспериментальной точки от заменяющей (аппроксимирующей) кривой. Квадраты отклонений берутся, чтобы компенсировать знаки «–» отклонений.
Для определенности задачи искомую функцию f(x) будем выбирать из класса алгебраических многочленов степени m:
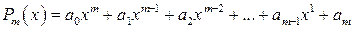 .
.
Назовем данный многочлен – аппроксимирующим многочленом. Аппроксимирующий многочлен не проходит через все узловые точки экспериментальных данных. Поэтому его степень m не зависит от числа узловых точек n. При этом всегда m < n. Степень m может меняться в пределах 1≤ m ≤ N-2.
Если m=1, то мы аппроксимируем табличную функцию прямой линией. Такая задача называется линейной регрессией.
Если m=2, то мы аппроксимируем табличную функцию квадратичной параболой. Такая задача называется квадратичной аппроксимацией.
Если m=3, то мы аппроксимируем табличную функцию кубической параболой. Такая задача называется кубической аппроксимацией.
Сумма S будет минимальной, если ее частные производные по параметрам ai равны нулю. Аналогично сумма S’ будет минимальной, если ее частные производные по параметрам C и k равны нулю. Произведя дифференцирование и соответствующие преобразования, получают систему нормальных уравнений, которая затем решается для нахождения искомой постоянной C и показателя степени k. Для обработки экспериментальных данных с целью получения аппроксимирующих функций используют компьютерные программы, реализующие метод наименьших квадратов. В частности программы EXCEL и MATHCAD, применение которых будет рассмотрено на практических занятиях.
Пример. Получены экспериментальные данные зависимости коэффициента напряженного состояния nσ от фактора формы очага деформации l/hc при прокатке высоких полос [28] (таб. 3.1).
Таблица 3.1
Экспериментальные данные зависимости коэффициента напряженного состояния nσ от фактора формы очага деформации l/hc
при прокатке высоких полос
| х=l/hc | 0,18 | 0,2 | 0,22 | 0,25 | 0,28 | 0,33 | 0,4 | 0,5 | 0,66 | 1,0 |
| у = nσ | 2,01 | 2,10 | 1,78 | 1,81 | 1,60 | 1,42 | 1,50 | 1,19 | 1,05 | 1,03 |
На рис. 3.5 представлены экспериментальные точки на поле будущего графика в EXCEL, а на рис. 3.6 аппроксимация логарифмической зависимостью у= 0,8582–0,6498ln(x), коэффициент корреляции 0,9. В работе [28] эта зависимость аппроксимирована формулой
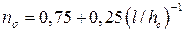 .
.
|
|
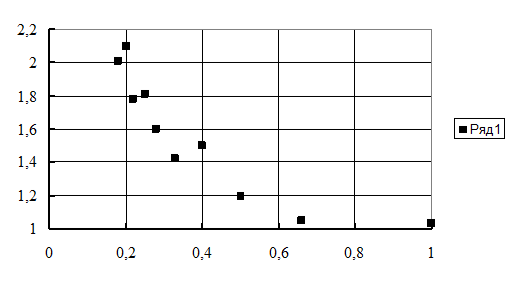
Рис. 3.5. Экспериментальные точки на графике, построенном в EXCEL
Путем изменения параметра х=l/hc на х=hc/l можно получить из нелинейной зависимости – линейную (таблица 3.2).
Таблица 3.2
Экспериментальные данные зависимости коэффициента напряженного состояния nσ от фактора формы очага деформации hc/l
при прокатке высоких полос
| х=hc/ l | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 |
| у = nσ | 1,03 | 1,05 | 1,19 | 1,50 | 1,42 | 1,60 | 1,81 | 1,78 | 2,10 | 2,01 |
|
|
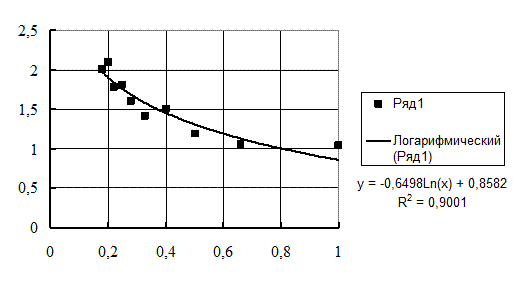
Рис. 3.6. Аппроксимация в EXCEL логарифмической зависимостью
у= 0,8582–0,6498lg(x)
На рис. 3.7 представлена линейная аппроксимация данных табл. 3.2.
|
|
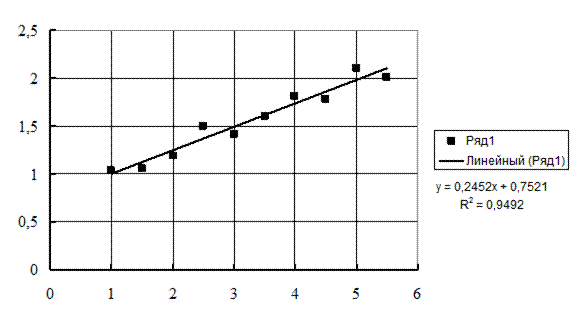
Рис. 3.7. Линейная аппроксимация зависимости коэффициента напряженного
состояния nσ от фактора формы очага деформации hc/l при прокатке высоких полос
Данный пример наглядно показывает, как правильный подбор параметров позволяет сделать зависимость линейной. В работе [28] эта зависимость аппроксимирована по методу избранных точек и методу средних (т.е. через две избранные точки) формулой 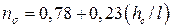 .
.
Дата добавления: 2017-01-26; просмотров: 2013;











