Предмет и теоретические основы вычислительного эксперимента

Компьютерное моделирование как новый метод научных исследований основывается на:

- математических моделях, описывающих изучаемый процесс;

- применении вычислительных машин, обладающих высоким быстродействием (миллионы операций в секунду) и способных вести диалог с человеком.

Исходя из того, что компьютерное моделирование применяется для исследования, оптимизации и проектирования реальных технологических объектов (систем), можно выделить следующие этапы этого процесса (рис. 3.1):

1) определение объекта – установление границ, ограничений и измерителей эффективности функционирования объекта;

2) формализация объекта (построение модели) – переход от реального объекта к некоторой логической схеме (абстрагирование);

3) подготовка данных – отбор данных, необходимых для построения модели, и представление их в соответствующей форме;

4) разработка моделирующего алгоритма и программы ЭВМ;

5) оценка адекватности – повышение до приемлемого уровня степени уверенности, с которой можно судить относительно корректности выводов о реальном объекте, полученных на основании обращения к модели;

6) стратегическое планирование – планирование вычислительного эксперимента, который должен дать необходимую информацию;

7) тактическое планирование – определение способа проведения каждой серии испытаний, предусмотренных планом эксперимента;

8) экспериментирование – процесс осуществления имитации с целью получения желаемых данных и анализа чувствительности;

9) интерпретация – построение выводов по данным, полученным путем имитации;

10) реализация – практическое использование модели и результатов моделирования;

11) документирование – регистрация хода осуществления процесса и его результатов, а также документирование процесса создания и использования модели.

В представленной на рис. 3.1 схеме организации процесса компьютерного моделирования (имитации) основная цепочка (реальный технологический объект (система) – математическая модель – моделирующий алгоритм – программа ЭВМ – вычислительный эксперимент) соответствует традиционной схеме, но во главу угла теперь ставится понятие триады: модель – алгоритм – программа(блоки 4, 5, 6), стратегическое и тактическое планирование вычислительного эксперимента (блок 7), интерпретация и документирование его результатов (блок 8).

Рис. 3.1. Схема организации компьютерного моделирования

Суть компьютерного моделирования состоит в следующем: на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель.

Например, располагая уравнением, описывающим протекание того или иного процесса, можно изменяя его коэффициенты, начальные и граничные условия, исследовать, как при этом будет вести себя объект. Более того, можно спрогнозировать поведение объекта в различных условиях.

Вычислительный эксперимент позволяет заменить дорогостоящий натурный эксперимент расчетами на ЭВМ. Он позволяет в короткие сроки и без значительных материальных затрат осуществить исследование большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации, что значительно сокращает сроки разработки сложных систем и их внедрение в производство.

Компьютерное моделирование и вычислительный эксперимент, как новый метод научного исследования, заставляет совершенствовать математический аппарат, используемый при построении математических моделей, позволяет, используя математические методы, уточнять, усложнять математические модели. Наиболее перспективным для проведения вычислительного эксперимента является его использование для исследования сложного комплекса явлений, характерных для пластической деформации металлов и сплавов – распределение скоростей, деформаций, температур, напряжений. Кроме того, вычислительный эксперимент позволяет на виртуальном объекте промоделировать различные технологические процессы и особенности их функционирования.

В некоторых процессах, где проведение натурных экспериментов требует больших материальных затрат, например, изготовление принципиально нового образца оборудования или проведение натурного эксперимента на действующих технологических линиях вычислительный эксперимент является единственно возможным подходом.

Для проверки адекватности математической модели и реального объекта, процесса или системы результаты исследований на ЭВМ сравниваются с результатами эксперимента на опытном натурном образце. Результаты проверки используются для корректировки математической модели или решается вопрос о применимости построенной математической модели к проектированию либо исследованию заданных объектов, процессов или систем.

Подчеркнем, компьютерное моделирование и вычислительный эксперимент позволяют свести исследование "нематематического" объекта к решению математической задачи. Этим самым открывается возможность использования для его изучения хорошо разработанного математического аппарата в сочетании с мощной вычислительной техникой. На этом основано применение математики и ЭВМ для познания законов реального мира и их использования на практике.

Решая прикладные задач на ЭВМ путем применения как точных методов решения, так и численных, необходимо помнить, что результаты вычислений носят приближенный характер. Важно только добиться того, чтобы ошибки укладывались в рамки требуемой точности.

Реальные процессы и системы можно исследовать с помощью двух типов математических моделей: аналитических и имитационных.

В аналитических моделях поведение реальных процессов и систем (РПС) задается в виде явных функциональных зависимостей (уравнений линейных или нелинейных, дифференциальных или интегральных, систем этих уравнений). Однако получить эти зависимости удается только для сравнительно простых РПС. Когда явления сложны и многообразны исследователю приходится идти на упрощенные представления сложных РПС. В результате аналитическая модель становится слишком грубым приближением к действительности. Если все же для сложных РПС удается получить аналитические модели, то зачастую они превращаются в трудно разрешимую проблему. Поэтому исследователь вынужден часто использовать имитационное моделирование [6].

Имитационное моделирование – численный метод проведения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими поведение реальных объектов, процессов и систем во времени в течении заданного периода. При этом функционирование РПС разбивается на элементарные явления, подсистемы и модули. Функционирование этих элементарных явлений, подсистем и модулей описывается набором алгоритмов, которые имитируют элементарные явления с сохранением их логической структуры и последовательности протекания во времени.

Имитационное моделирование – это совокупность методов алгоритмизации функционирования объектов исследований, программной реализации алгоритмических описаний, организации, планирования и выполнения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими функционирование РПС в течении заданного периода.

Под алгоритмизацией функционирования понимается пооперационное описание работы всех ее функциональных подсистем отдельных модулей с уровнем детализации, соответствующем комплексу требований к модели.

"Имитационное моделирование" (ИМ)- это двойной термин. "Имитация" и "моделирование" - это синонимы. Фактически все области науки и техники являются моделями реальных процессов. Чтобы отличить математические модели друг от друга, исследователи стали давать им дополнительные названия. Термин "имитационное моделирование" означает, что мы имеем дело с такими математическими моделями, с помощью которых нельзя заранее вычислить или предсказать поведение системы, а для предсказания поведения системы необходим вычислительный эксперимент (имитация) на математической модели при заданных исходных данных.

Основное достоинство ИМ:

– возможность описания поведения компонент (элементов) процессов или систем на высоком уровне детализации;

– отсутствие ограничений между параметрами ИМ и состоянием внешней среды РПС;

– возможность исследования динамики взаимодействия компонент во времени и пространстве параметров системы;

Эти достоинства обеспечивают имитационному методу широкое распространение.

Рекомендуется использовать имитационное моделирование в следующих случаях:

1. Если не существует законченной постановки задачи исследования и идет процесс познания объекта моделирования. Имитационная модель служит средством изучения явления.

2. Если аналитические методы имеются, но математические процессы сложны и трудоемки, и имитационное моделирование дает более простой способ решения задачи.

3. Когда кроме оценки влияния параметров (переменных) процесса или системы желательно осуществить наблюдение за поведением компонент (элементов) процесса или системы (ПС) в течение определенного периода.

4. Когда имитационное моделирование оказывается единственным способом исследования сложной системы из-за невозможности наблюдения явлений в реальных условиях (реакции термоядерного синтеза, исследования космического пространства).

5. Когда необходимо контролировать протекание процессов или поведение систем путем замедления или ускорения явлений в ходе имитации.

6. При подготовке специалистов новой техники, когда на имитационных моделях обеспечивается возможность приобретения навыков в эксплуатации новой техники.

7. Когда изучаются новые ситуации в РПС. В этом случае имитация служит для проверки новых стратегий и правил проведения натурных экспериментов.

8. Когда особое значение имеет последовательность событий в проектируемых ПС и модель используется для предсказания узких мест в функционировании РПС.

Однако ИМ наряду с достоинствами имеет и недостатки:

1. Разработка хорошей ИМ часто обходится дороже создания аналитической модели и требует больших временных затрат.

2. Может оказаться, что ИМ неточна (что бывает часто), и мы не в состоянии измерить степень этой неточности.

3. Зачастую исследователи обращаются к ИМ, не представляя тех трудностей, с которыми они встретятся и совершают при этом ряд ошибок методологического характера.

И тем не менее ИМ является одним из наиболее широко используемых методов при решении задач синтеза и анализа сложных процессов и систем.

Одним из видов имитационного моделирования является статистическое имитационное моделирование, позволяющее воспроизводить на ЭВМ функционирование сложных случайных процессов.

При исследовании сложных систем, подверженных случайным возмущениям используются вероятностные аналитические модели и вероятностные имитационные модели.

В вероятностных аналитических моделях влияние случайных факторов учитывается с помощью задания вероятностных характеристик случайных процессов (законы распределения вероятностей, спектральные плотности или корреляционные функции). При этом построение вероятностных аналитических моделей представляет собой сложную вычислительную задачу. Поэтому вероятностное аналитическое моделирование используют для изучения сравнительно простых систем.

Подмечено, что введение случайных возмущений в имитационные модели не вносит принципиальных усложнений, поэтому исследование сложных случайных процессов проводится в настоящее время, как правило, на имитационных моделях.

В вероятностном имитационном моделировании оперируют не с характеристиками случайных процессов, а с конкретными случайными числовыми значениями параметров ПС. При этом результаты, полученные при воспроизведении на имитационной модели рассматриваемого процесса, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется его многократное воспроизведение, с последующей статистической обработкой полученных данных. Именно поэтому исследование сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационного моделирования принято называть статистическим моделированием.

Статистическая модель случайного процесса – это алгоритм, с помощью которого имитируют работу сложной системы, подверженной случайным возмущениям; имитируют взаимодействие элементов системы, носящих вероятностный характер.

При реализации на ЭВМ статистического имитационного моделирования возникает задача получения на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками. Численный метод, решающий задачу генерирования последовательности случайных чисел с заданными законами распределения получил название "метод статистических испытаний" или "метод Монте-Карло".

Итак, статистическое моделирование – это способ изучения сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационных моделей.

Этапы методики статистического моделирования:

1. Моделирование на ЭВМ псевдослучайных последовательностей с заданной корреляцией и законом распределения вероятностей (метод Монте-Карло), имитирующих на ЭВМ случайные значения параметров при каждом испытании;

2. Преобразование полученных числовых последовательностей на имитационных математических моделях.

3. Статистическая обработка результатов моделирования.

Алгоритм метода статистических испытаний представлен на 2.13.

Рассмотрение основ теории и различных статистических методов решения технологических задач ОМД дано в работе [26].

Рис. 2.13. Обобщенный алгоритм метода статистических испытаний

Пример.Напряжения трения при горячей осадке полосы с поперечным сечением b×h являются статистической функцией, зависящей от колебаний температур нагрева заготовки и инструмента, колебаний механических свойств заготовки и условий на поверхности контакта (смазка, окалина). В этих условиях закон трения можно принять в следующем виде [13]

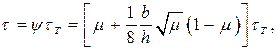,(3.1)

где ψ – детерминированная функция, зависящая от формы очага деформации b/h и коэффициента трения μ; τ_Т – случайная величина предела текучести на сдвиг на поверхности заготовки, зависящая от случайной температуры θ(τ_Т = 1,74 – 0,0118θ).

Применив к (3.1) операторы образования начальных и центральных моментов функций [26] получим:

– математическое ожидание напряжения трения

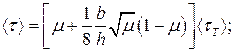
– дисперсию напряжения трения

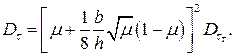
Так при осадке заготовки из стали 45 при b/h = 1, скорости деформирования v_и/h = 0,3 с^-1 и θ = 1200⁰С значения случайной скорости деформации ξ₁₁ колеблются в следующих пределах: ξ₁₁ = 0,42±0,08 (при D_τ= 1,0 МПа²); ξ₁₁ = 0,42±0,17 (при D_τ= 4,0 МПа²).

Основными параметрами, определяющими меру случайности (стабильность) полей скоростей в процессе осадки полосы, являются форма очага деформации, величина дисперсии предела текучести на сдвиг, реологические свойства, температура обрабатываемого материала и скорость деформирования.

Имитационное моделирование достаточно широко применяется при анализе систем массового обслуживания и надежности систем различного назначения [27].