Метод наименьших квадратов

Пусть по выборке (x_i, y_i) требуется определить оценки коэффициентов b₀ и b₁ эмпирического уравнения регрессии (5.8). В случае использования МНК минимизируется следующая функция потерь:

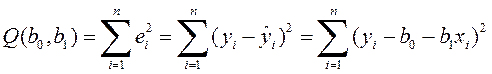. (10)

Нетрудно заметить, что функция Q является квадратичной функцией двух параметров b₀ и b₁, поскольку x_i и y_i – известные данные наблюдений. Поскольку функция Q непрерывна, выпукла и ограничена снизу (Q³0), то она имеет минимум.

Необходимым условием существования минимума функции двух переменных (10) является равенство нулю ее частных производных по неизвестным параметрам b₀ и b₁:

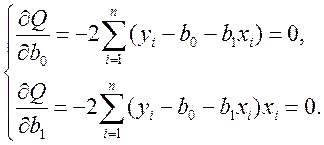(11)

После преобразований получим систему нормальных уравнений (систему линейных алгебраических уравнений) для определения параметров простой линейной регрессии:

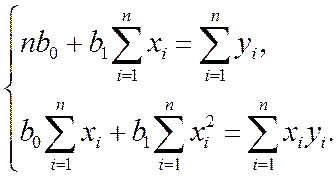(12)

Разделив оба уравнения на n, получим:

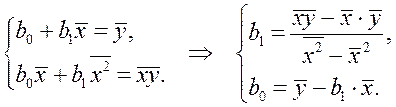(13)

Здесь 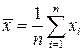, , 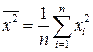, 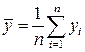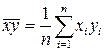. Таким образом, оценки параметров простой линейной регрессии по МНК определяются по формулам (13).

Нетрудно заметить, что b₁ можно вычислить по формуле

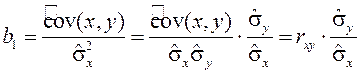, (14)

где r_xy – выборочный коэффициент корреляци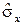и, и 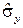– средние квадратичные отклонения.

Таким образом, коэффициент регрессии b₁ пропорционален коэффициенту корреляции. Следовательно, если коэффициент корреляции r_xy уже рассчитан, то легко может быть найден коэффициент регрессии b₁ по формуле (14).

Отметим, что кроме уравнения регрессии Y на X: ,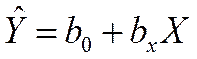

для тех же эмпирических данных может быть найдено уравнение регрессии X на Y: .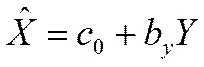

Коэффициенты регрессии b_x и b_y в этом случае будут связаны равенством:

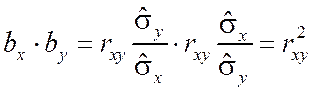. (15)

Подставляя значения b₀ и b₁, вычисленные по формулам (13), в (8), получим уравнение линейной регрессии Y на X:

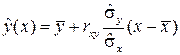. (16)

Аналогично можно получить уравнение линейной регрессии X на Y:

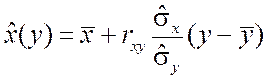. (17)

Можно заметить, что обе прямые регрессии пересекаются в точке 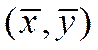. Причем, чем больше коэффициент корреляции, тем меньше угол φ между прямыми (рис. 2).

В частности, если r=±1, то обе прямые регрессии совпадут. Если коэффициент корреляции равен нулю, то линии регрессии будут параллельны координатным осям.

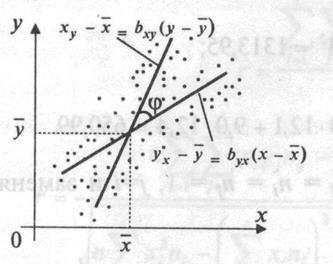
Рис. 2

Полученные формулы для коэффициентов регрессии позволяют сделать ряд выводов:

1. Эмпирическая прямая регрессии обязательно проходит через точку .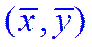

2. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений 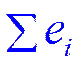, а также среднее значение отклонений равны нулю.

% Действительно, из формулы 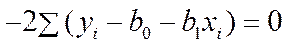в соотношении (11) следует, что .

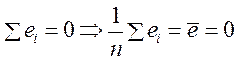3. Случайные отклонения e_i не коррелированы с наблюдаемыми значениями y_i зависимой переменной Y.

Для обоснования данного утверждения покажем, что ковариация между Y и e равна нулю. Действительно,

.

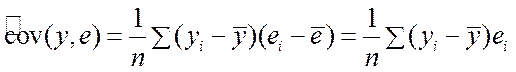Покажем, что 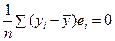. Просуммировав по i все соотношения (9), получим:

,

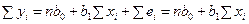т.к. 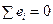. Разделив последнее соотношение на n, получим 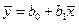. Вычитая из (5.9) полученное соотношение, приходим к следующей формуле:

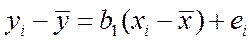. (5.18)

Тогда

.

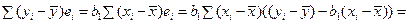
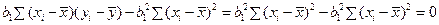Следовательно, . &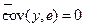

4. Случайные отклонения e_i не коррелированы с наблюдаемыми значениями x_i независимой переменной X.

% Действительно, 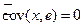в силу второй формулы системы (5.11). &

Для иллюстрации МНК рассмотрим следующий пример,