Метод наименьших квадратов

Важным приложением теории экстремумов функции нескольких переменных является построение эмпирических зависимостей методом наименьших квадратов.

Решение многих практических задач из различных областей науки и техники часто приводит к необходимости строить так называемые эмпирические зависимости (от греч. emptiria (εμπιρια) – опыт), т.е. по данным опыта, эксперимента, подсчета установить форму связи между двумя переменными величинами (формулу, связывающую эти переменные).

Пусть в результате эксперимента получено п значений переменной величины х и соответствующих им значений величины у:

Вид аппроксимирующей функции у = f(x) , связывающей переменные величины х и у, можно подобрать или из теоретических соображений, или на основании характера расположения точек (х₁, у₁), (х₂, у₂), ...., (х_п, у_п) на координатной плоскости (в случае небольшого количества экспериментальных данных в системе координат их можно отметить вручную, если данных много – можно использовать компьютерные технологии).

Например, для экспериментальных данных, изображенных на рисунке 8а, естественно предположить что зависимость между переменными х и у линейная, т.е. искать аппроксимирующую функцию у = f(x) в виде у = ах + b , где а и b некоторые параметры, которые нужно подобрать так, чтобы значения у(х_i) = ах_i + b, вычисленные по выбранной формуле, как можно меньше отличались от соответствующих х_i экспериментальных значений у_i.

Для данных, изображенных на рисунке 8б, зависимость можно искать в виде y = ax² + bx + c, или в виде у = а^х+b и по величине отклонений эмпирических значений у_i от вычисленных по формуле можно выбрать ту из функций, которая наилучшим образом описывает эмпирическую зависимость (ту, для которой эти отклонения – наименьшие)

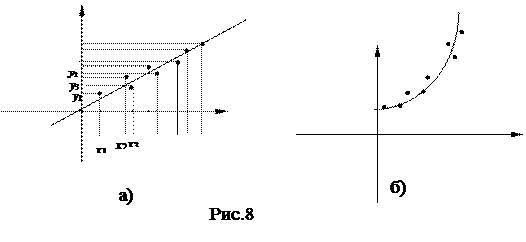Одним из методов решения такой задачи и является метод наименьших квадратов. Суть этого метода в следующем.

Пусть в качестве эмпирической выбрана формула у = f(x, a, b, с...). Рассмотрим сумму квадратов разностей экспериментальных значений у_i и значений аппроксимирующей функции f(x, a, b, с ...) в соответствующих точках х_i:

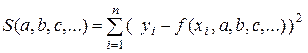
и подберем параметры a, b, с ... так, чтобы эта сумма имела наименьшее значение:

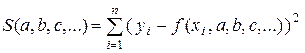= min.

Таким образом, задача свелась к отысканию таких значений параметров a, b, с ... , при которых функция S(a, b, с ...) имеет минимум. Согласно теореме 9.1, функция S(a, b, с ...) нескольких переменных имеет экстремум в точках, где ее частные производные первого порядка по всем аргументам равны нулю (так как функция – квадратичная, то ее производные существуют для всех значений аргументов), т.е.

, ... .

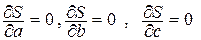В развернутом виде эти условия имеют вид

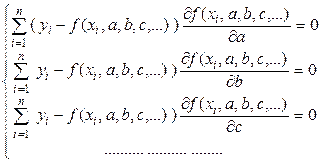
Заметим, что в каждом конкретном случае необходимо исследовать вопрос о существовании решения этой системы и наличии минимума функции S(a, b, с ...). Пример решения такой задачи рассмотрен в практических занятиях.