Возможности программы Deform 3D.
DEFORM - 3D является системой конечно-элементного моделирования разрабатываемой компанией Scientific Forming Technologies Corporation (SFTC), и предназначена для анализа трехмерного течения металла при различных процессах обработки металлов давлением. Данная система позволяет прогнозировать характер формоизменения с высокой точностью и минимальными затратами на экспериментальные проверки. Ниже перечислены операции которые возможно моделировать в Deform:
- ковка;
- выдавливание;
- протяжка;
- механообработка;
- высадка;
- прессование;
- прокатка;
- вытяжка;
- осадка.
В данной программе есть собственный сеточный построитель, который производит полностью автоматическое разбиение сетки конечных элементов во время моделирования (адаптивное перестроение сетки) и присутствует библиотека оборудования для горячей и холодной штамповки.
Модели материалов используемые в программе могут быть следующих типов: жесткие, пластичные, упруго-пластичные, пористые, упругие.
Конечные элементы и модели материалов позволяют отслеживать места разрушения материалов. Для сложных переходных процессов присутсвует возможность задавать параметры многопереходных процессов (рис. 4.9).
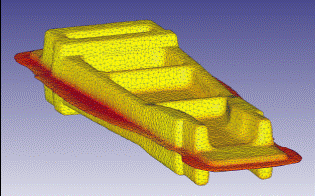
Рис. 4.9. Анализ кованой детали в Deform
Кроме анализа напряжений, деформаций и температур в заготовке и инструменте, в программе предусмотрена возможность определения энергетических и силовых параметров оборудования.
Главным преимуществом системы Deform перед универсальными конечно-элементными пакетами типа Ansys, LS-Dyna или MSC-Marc является ее объектная ориентированность, что позволяет ее легко осваивать специалисту никогда прежде не использовавшего МКЭ в своей практике. Подобная технологическая ориентация данной программы прослеживается во всей структуре программы и позволяет исследователю в области ОМД легко ориентироваться в инструментарии программы благодаря привычным терминам.
Следует отметить, что расчет процессов ОМД может осуществляться не только в специализированных пакетах программ, но и в доступных математических пакетах – MathLAB и MathCAD (использование дано в практикуме). При использовании этих пакетов целесообразно производить моделирования процессов, которые описываются аналитически, то есть отработанных методик. Данные пакеты обладают обширным функционалом для автоматизации вычислений и позволяют легко построить аналитическую схему вычисления, например для установившегося процесса прокатки.
Другим путем разработки сложных численных алгоритмов решения задач ОМД может быть использование специальных средств разработки, таких как Diffpack, который, является профессиональным объектно-ориентированным и проблемно-решающим окружением для численного решения дифференциальных уравнений в частных производных и разработки независимых приложений.
Уникальность программы Diffpack заключается в его возможностях. Данная пакет программ является объектно-ориентированным окружением, работающим под С++, предназначенным для решения дифференциальных уравнений в частных производных. Он представляет собой совокупность текстов программ, написанных на языке C++, и библиотек, что позволяет с минимальными затратами времени создавать консольные приложения или приложения Windows для решения уравнения или системы уравнений в частных производных. В программе реализован новый подход к решению задач математической физики за счет того, что пользователь сам может задавать решаемое уравнение или систему дифференциальных уравнений в частных производных.В программе есть возможность интеграции с существующим программным обеспечением и связь с FORTRAN программами. Для решения дифференциальных уравнений в частных производных в программе предусмотрен широкий выбор методов решения – метод конечных элементов, метод конечных разностей, конечных объемов и их различные модификации с аппроксимациями функций высокого порядка. Для эффективного решения присутствуют алгоритмы адаптивного сгущения сеток, декомпозиции областей, распараллеливания вычислений, многосеточных методов, а также высокоэффективные алгоритмы решения СЛАУ. В программе присутствуют широкие возможности для анализа и обработки данных и отображения результатов вычисления. Предусмотрена поддержка взаимодействия с ANSYS, Abaqus, и другими CAE.
При выполнения практикума предусмотрены работы по освоению пакета ANSYS и LS-DUNA.
Ниже приведены примеры использования МКЭ при решении различных задач [33].
5. Постановка и методы решения задач Оптимизации
5.1. Общая постановка задач оптимизации
При проектировании любых технических объектов, технологических процессов и систем всегда решаются задачи выбора и принятия решений.
Задачей принятия решения называют кортеж (совокупность)

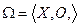 ,
,
где X – множество вариантов решения задачи;
O – принцип оптимальности, дающий представление о качестве вариантов, в простейшем случае – это правило их предпочтения друг перед другом.
Решением задачи принятия решений называется множество 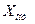 , которое является подмножеством множества
, которое является подмножеством множества 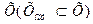 , полученное на основе принципа оптимальности.
, полученное на основе принципа оптимальности.
Задачи принятия решений классифицируются по наличию информации об X и O и бывают трех видов:
1. X и O – неизвестны. Это общая задача принятия решений. Данные для получения xопт определяют в данной задаче в процессе ее решения.
2. X –неизвестно, O – известно ( эта задача поиска вариантов).
3. X и O – известны (это задача оптимизации).
В общем случае задача принятия решения решается в два этапа:
1 этап: Задача формализуется, т.е. строится ее математическая модель, в которой конкретные физические, технические, технологические, экономические условия и требования к объекту воплощаются в виде задачи оптимизации с определенной целевой функцией и допустимым множеством вариантов.
2 этап: Решение задачи оптимизации с использованием известных методов.
Рассмотрим основы теории оптимизации. «Теория оптимизации», с одной стороны, является самостоятельной наукой, а, с другой стороны, составной частью науки под названием «исследование операций».
Операция (в данной науке) – это совокупность взаимосогласованных действий, направленных на достижение вполне определенной цели.
Обязательно должно быть сформулирована цель. Если есть разные пути достижения этой цели, то необходимо найти наилучший из них.
Постановка задачи оптимизации включает в себя множество допустимых решений 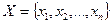 и числовую функцию f, определенную на этом множестве, которая называется целевой функцией.
и числовую функцию f, определенную на этом множестве, которая называется целевой функцией.
Нельзя отождествлять критерий (критерии) оптимальности и целевую функцию.
Целевая функция – это аналитическая зависимость между критерием (критериями) оптимальности и подлежащими оптимизации параметрами с указанием направления экстремума.
Выбор критериев – сложная задача, т.к. цели при проектировании любого объекта, как правило, противоречивы (обеспечение минимальной стоимости и максимальной надежности, максимальной производительности и минимальной энергоемкости и т.д.).
Если требуется оптимизировать один из показателей качества проектируемого объекта при соблюдении ограничительных требований на остальные показатели, то нужно сформировать один частный критерий. Задача оптимизации при этом сводится к задаче максимизации (минимизации) данного критерия с учетом заданных ограничений.
При наличии нескольких критериев выбирают:
а) аддитивный критерий, если существенное значение имеют абсолютные значения критериев при выбранном векторе параметров X;
б) мультипликативный критерий, если существенную роль играет изменение абсолютных значений частных критериев при вариации вектора X;
в) максиминный (минимаксный) критерий, если стоит задача достижения равенства нормированных значений противоречивых (конфликтных) частных критериев.
Отличие понятий «критерий» и «целевая функция» состоит в следующем:
1. Целевая функция может включать в себя более одного критерия.
2. Для целевой функции всегда и обязательно указывается вид экстремума:
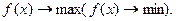
Различают два вида задач оптимизации:
1. Задачу минимизации.
2. Задачу максимизации.
Чтобы решить задачу минимизации функции f на множестве X, необходимо найти такой вектор 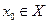 ( а также соответствующее значение целевой функции
( а также соответствующее значение целевой функции 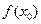 ), чтобы неравенство:
), чтобы неравенство: 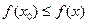 выполнялось для всех
выполнялось для всех 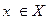 . При этом x0 называют оптимальным решением (точнее здесь – минимальным решением), а
. При этом x0 называют оптимальным решением (точнее здесь – минимальным решением), а 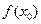 - оптимумом (минимумом).
- оптимумом (минимумом).
Чтобы решить задачу максимизации функции f на множестве X, необходимо найти такой вектор 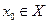 (а также соответствующее значение целевой функции
(а также соответствующее значение целевой функции 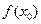 ), чтобы неравенство:
), чтобы неравенство: 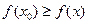 выполнялось для всех
выполнялось для всех 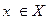 . При этом x0 называют оптимальным (максимальным) решением, а
. При этом x0 называют оптимальным (максимальным) решением, а 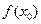 – оптимумом (максимумом).
– оптимумом (максимумом).
В общем виде находится именно вектор x0, т.к., например, при решении двухпараметрической задачи, он будет включать в себя два параметра, трехпараметрической – три параметра и т.д.
Локальный и глобальный минимум (максимум) целевой функции.
При решении задач оптимизации следует иметь в виду, какой вид имеет целевая функция.
Например, 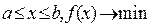 . Целевая функция имеет вид, как показано на рис. 5.1. Здесь точка x0 - глобальный минимум, а точка x1 - локальный минимум целевой функции.
. Целевая функция имеет вид, как показано на рис. 5.1. Здесь точка x0 - глобальный минимум, а точка x1 - локальный минимум целевой функции.
Пусть теперь 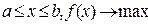 , а целевая функция имеет вид, как показано на рис.5.2. Здесь точка x0 - глобальный максимум, а точка x1 - локальный максимум целевой функции.
, а целевая функция имеет вид, как показано на рис.5.2. Здесь точка x0 - глобальный максимум, а точка x1 - локальный максимум целевой функции.
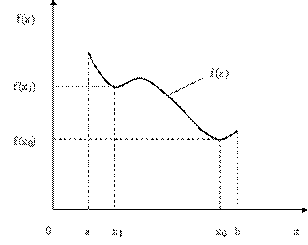
Рис.5.1. Иллюстрация понятий «локальный минимум» и «глобальный минимум» целевой функции
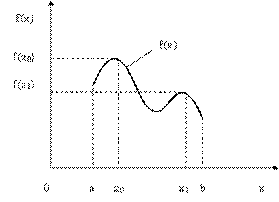
Рис.5.2. Иллюстрация понятий «локальный максимум» и «глобальный максимум» целевой функции
Разрешимость задач оптимизации.
Приведенная выше задача оптимизации имеет решение не при любых целевых функциях и допустимых множествах. Существуют задачи, в которых невозможно найти оптимальное решение и экстремум целевой функции. Например, не существует точек минимума функции одной переменной f на множестве 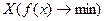 в случаях, приведенных ниже на рис. 5.3, 5.4 и 5.5.
в случаях, приведенных ниже на рис. 5.3, 5.4 и 5.5.
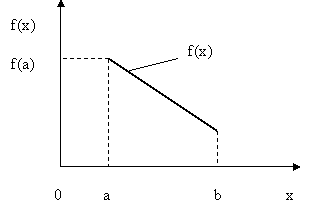
Рис.5.3. Иллюстрация случая, когда множество допустимых решений не замкнуто
Здесь граница «а» множества допустимых решений в интервал входит, а граница «b» нет.
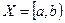 - множество X не замкнуто, следовательно,
- множество X не замкнуто, следовательно, 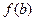 – не существует.
– не существует.
В случае, представленном на рис.5.4, определена лишь одна левая граница множества допустимых решений. 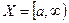 , т.е. множество допустимых решений неограниченно.
, т.е. множество допустимых решений неограниченно.
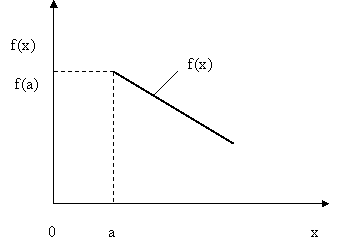
Рис.5.4. Иллюстрация неограниченности множества допустимых решений
На рис. 5.5. показан еще один случай, когда задача оптимизации не имеет однозначного решения.
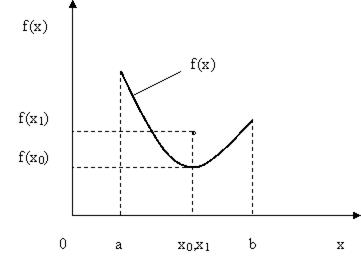
Рис.5.5. Иллюстрация случая, когда функция f(x) не является непрерывной
Здесь функция 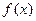 не является непрерывной, т.к. в точке
не является непрерывной, т.к. в точке 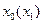 существуют два значения функции –
существуют два значения функции – 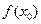 и
и 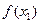 .
.
Следовательно, задача оптимизации разрешима, если выполняются следующие три условия:
1. Множество допустимых решений X замкнуто, т.е. если предельные точки принадлежат этому множеству.
2. Множество X ограничено.
3. Целевая функция 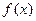 непрерывна.
непрерывна.
Это нестрогая формулировка теоремы Вейерштрасса [34].
Определение. Пусть на множестве u, состоящем из элементов u линейного метрического пространства определена скалярная функция Φ(u).
1. Говорят, что Φ(u) имеет локальный минимум на элементе u*, если существует его конечная ε - окрестность, в которой выполнено
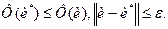 (5.1)
(5.1)
2. Φ(u) достигает глобального минимума в u на элементе u* (строгий, абсолютный минимум), если имеет место равенство
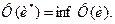 (5.2)
(5.2)
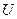
Замечание. Если u - числовая ось, решается задача на нахождение минимума функции одного переменного, если u – n-мерное векторное пространство, имеется задача на нахождение минимума функции n переменных, если u – функциональное пространство, то решается задача на отыскание функции, доставляющей минимум функционалу (задача оптимального управления или динамического программирования).
Если к (5.1) или (5.2) добавляются условия
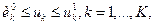
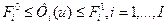
( 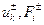 - числа, a Φi - заданные функции), то это задача поиска условного минимума, если подобные ограничения отсутствуют, то это задача поиска безусловного минимума. Причем, если функции Φi(u) линейны, задача поиска условного минимума называется задачей линейного программирования, если хотя бы одна из этих функций нелинейна, то имеется задача нелинейного программирования. Обе эти задачи вместе с задачей динамического программирования в теории оптимального управления называются задачами математического программирования.
- числа, a Φi - заданные функции), то это задача поиска условного минимума, если подобные ограничения отсутствуют, то это задача поиска безусловного минимума. Причем, если функции Φi(u) линейны, задача поиска условного минимума называется задачей линейного программирования, если хотя бы одна из этих функций нелинейна, то имеется задача нелинейного программирования. Обе эти задачи вместе с задачей динамического программирования в теории оптимального управления называются задачами математического программирования.
Рассмотрим классификацию численных методов решения задач нелинейного программирования:
1. Численные методы поиска экстремума функции одной переменной.
1.1. Классический метод.
1.2. Метод равномерного перебора.
1.3. Метод золотого сечения.
1.4. Метод Фибоначчи и т.д.
2. Численные методы поиска экстремума функции n – переменных.
2.1. Численные методы в задачах без ограничений.
2.1.1. Метод покоординатного спуска.
2.1.2. Метод Хука – Дживса.
2.1.3. Градиентный метод.
2.1.4. Метод Ньютона.
2.1.5. Метод сопряженных направлений и т.д.
2.2. Численные методы в задачах с ограничениями.
2.2.1. Метод покоординатного спуска.
2.2.2. Метод условного градиента.
2.2.3. Метод барьерных функций.
2.2.4. Метод штрафных функций.
2.2.5. Метод линеаризации и т.д.
Универсального метода, с помощью которого можно было бы решить любую задачу оптимизации, не существует. Поэтому для решения конкретной задачи применяют один или несколько своих численных методов.
5.2. Численные методы решения задач одномерной оптимизации
Методы поиска экстремума функции одной переменной
Эти методы применяются в однопараметрических задачах оптимизации. В них ищется один оптимальный параметр. Целевая функция – это функция одной переменной.
Постановка задачи. Найти значение переменной x, доставляющее минимум или максимум целевой функции 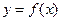 , при условиях
, при условиях 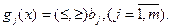 .
.
Рассмотрим классический метод минимизации (максимизации) функции одной переменной.
Пусть 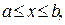 функция
функция 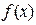 непрерывна на этом отрезке и имеет на нем непрерывную производную. Вычисляют значение производной
непрерывна на этом отрезке и имеет на нем непрерывную производную. Вычисляют значение производной 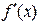 и определяют критические точки, т.е. такие внутренние точки отрезка
и определяют критические точки, т.е. такие внутренние точки отрезка 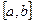 , в которых производная обращается в нуль или не существует. В окрестности каждой такой критической точки исследуют знак производной и отбирают те из них, при переходе через которые производная меняет знак с минуса на плюс (это точки локального минимума) или с плюса на минус (это точки локального максимума ). Затем вычисляют значения целевой функции в этих точках и на границах отрезка
, в которых производная обращается в нуль или не существует. В окрестности каждой такой критической точки исследуют знак производной и отбирают те из них, при переходе через которые производная меняет знак с минуса на плюс (это точки локального минимума) или с плюса на минус (это точки локального максимума ). Затем вычисляют значения целевой функции в этих точках и на границах отрезка 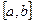 . Эти значения сравнивают между собой и определяют точку, в которой достигается минимум (максимум) целевой функции. Эта точка является точкой глобального минимума (максимума) функции
. Эти значения сравнивают между собой и определяют точку, в которой достигается минимум (максимум) целевой функции. Эта точка является точкой глобального минимума (максимума) функции 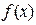 на отрезке
на отрезке 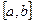 .
.
При решении реальных задач оптимизации данный метод применяется редко, т.к. зачастую производную целевой функции определить сложно или невозможно.
Метод равномерного перебора.
Пусть дана функция 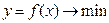 (см. рис 5.6).
(см. рис 5.6).
В соответствии с данным методом алгоритм поиска 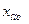 заключается в следующем. Фиксируют величину шага h > 0. Вычисляют значения целевой функции в точках
заключается в следующем. Фиксируют величину шага h > 0. Вычисляют значения целевой функции в точках 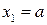 и
и 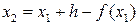 и
и 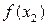 . Полученные значения сравнивают. Запоминают меньшее из этих двух значений. Далее выбирается точка
. Полученные значения сравнивают. Запоминают меньшее из этих двух значений. Далее выбирается точка 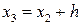 и в ней вычисляется значения целевой функции
и в ней вычисляется значения целевой функции 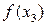 . Сравнивается оставшееся на предыдущем шаге значение и значение
. Сравнивается оставшееся на предыдущем шаге значение и значение 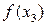 . Наименьшее из них опять запоминают. Так поступают до тех пор, пока очередное значение
. Наименьшее из них опять запоминают. Так поступают до тех пор, пока очередное значение 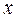 не превысит
не превысит 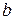 . Последнее оставшееся значение является приближенным значением глобального минимума.
. Последнее оставшееся значение является приближенным значением глобального минимума.
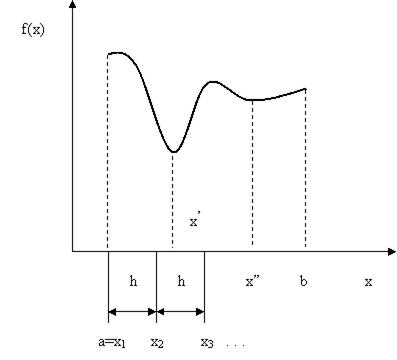
Рис. 5.6. Графическая иллюстрация метода равномерного перебора
Трудности при использовании данного метода. Если целевая функция имеет узкую впадину, подобную приведенной на рис. 5.6, то можно ее проскочить, и вместо точки глобального минимума определить точку локального минимума. Т.е. вместо 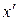 можно найти
можно найти 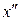 . Эта проблема частично снимается, если выбрать очень маленький шаг, но при этом потребуется много времени (в том числе и машинного) для решения задачи.
. Эта проблема частично снимается, если выбрать очень маленький шаг, но при этом потребуется много времени (в том числе и машинного) для решения задачи.
Метод золотого сечения.
Рассматриваемая в данном методе функция должна быть унимодальной. Функция 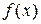 является унимодальной на отрезке
является унимодальной на отрезке 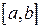 , если она на этом отрезке имеет единственную точку глобального минимума и слева от этой точки является строго убывающей, а справа строго возрастающей.
, если она на этом отрезке имеет единственную точку глобального минимума и слева от этой точки является строго убывающей, а справа строго возрастающей.
Суть метода золотого сечения заключается в том, чтобы определить точку глобального минимума на отрезке 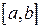 за минимальное количество шагов, т.е. за минимальное количество вычислений целевой функции.
за минимальное количество шагов, т.е. за минимальное количество вычислений целевой функции.
В соответствии с данным методом в каждый текущий момент времени рассматривается всегда две точки, например, в начальный момент точки 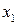 и
и 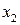 так, чтобы
так, чтобы 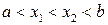 . При этом возможен один из двух случаев (рис.5.7).
. При этом возможен один из двух случаев (рис.5.7).
Согласно свойству унимодальной функции в первом случае искомая точка xmin не может находиться на отрезке [x2, b], во втором случае на отрезке [a, x1] (показаны штриховкой). Значит, область поиска сужается,
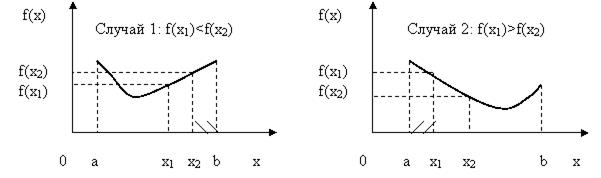
Рис.5.7. Иллюстрация обоснования исключения отрезков
и следующую точку x3 необходимо брать на одном из укороченных отрезков: [a, x2] - случай 1 или [x1, b] - случай 2.
Теперь следует определиться, где на исходном отрезке [a, b] необходимо выбирать точки 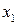 и
и 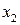 . Первоначально ничего не известно о положении точки xmin (графиков нет, и они не строятся, здесь мы их приводим для наглядной иллюстрации сути метода, при реальной оптимизации есть только выражение для целевой функции). Поэтому любой из приведенных выше случаев возможен с одинаковой вероятностью. Это означает, что лишним может оказаться любой из отрезков: [x2, b] или [a, x1]. Отсюда ясно, что точки
. Первоначально ничего не известно о положении точки xmin (графиков нет, и они не строятся, здесь мы их приводим для наглядной иллюстрации сути метода, при реальной оптимизации есть только выражение для целевой функции). Поэтому любой из приведенных выше случаев возможен с одинаковой вероятностью. Это означает, что лишним может оказаться любой из отрезков: [x2, b] или [a, x1]. Отсюда ясно, что точки 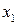 и
и 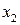 следует выбирать симметрично относительно середины отрезка [a, b].
следует выбирать симметрично относительно середины отрезка [a, b].
Далее для того, чтобы максимально сузить область поиска, эти точки должны быть поближе к середине исходного отрезка. Однако слишком близко к середине отрезка их тоже брать не следует, т.к. мы хотим построить алгоритм, для реализации которого необходимо общее минимальное количество вычислений целевой функции. Рассмотрим рис. 5.8.
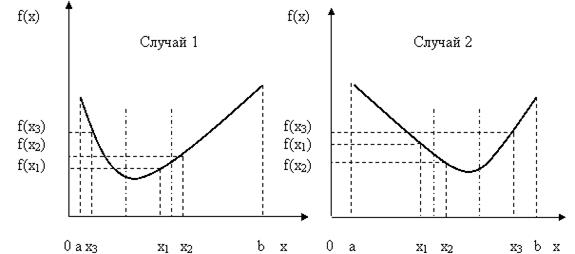
Рис.5.8. Иллюстрация обоснования расположения точек на отрезке
Выбирая на первом шаге сравниваемые точки слишком близко к середине отрезка [a, b], мы исключим из рассмотрения большой отрезок [x2, b] для случая 1 или [a, x1] для случая 2. Но на втором шаге величина исключаемого отрезка значительно уменьшится (будет исключен отрезок [a, x3] для случая 1 или отрезок [x3, b] для случая 2).
Таким образом, с одной стороны, точки следует брать рядом с серединой отрезка, а, с другой стороны, слишком близко друг от друга их брать нельзя. Т.е. необходимо найти некую «золотую середину».Для этого рассмотрим для простоты вместо отрезка [a, b] отрезок [0,1] единичной длины – рис.5.9.

Рис.5.9. Обоснование «золотой середины» расположения точек на отрезке
На этом рисунке |AB|=|CD|=x, |AC|=|BD|=1-x, |DC|=1-2x.
Для того, чтобы точка B была «выгодной» как на данном , так и на следующем этапе (шаге), она должна делить отрезок AD в таком же отношении, как и AC: AB/AD = BC/AC. При этом в силу симметрии аналогичным свойством будет обладать и точка C: CD/AD = BC/BD. В обозначениях координаты x эти пропорции принимают вид: x/1 = (1 – 2x)/(1 – x). Решим эту пропорцию:
x(1-x)=1-2x → x –x2 =1-2x → x- x2-1+2x=0 → - x2+ 3x-1=0 → x2- 3x+1=0,
Д = b2 – 4ac = 9 – 4 =5.
Корни этого уравнения равны:
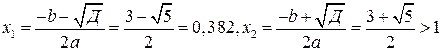
не приемлем, т.е. уравнение имеет один корень.
О точке, которая расположена на расстоянии 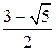 длины от одного из концов отрезка, говорят, что она осуществляет «золотое сечение» данного отрезка.
длины от одного из концов отрезка, говорят, что она осуществляет «золотое сечение» данного отрезка.
Очевидно, что каждый отрезок имеет две такие точки, расположенные симметрично относительно его середины.
Итак, алгоритм метода «золотого сечения» заключается в следующем (см. также рис.5.7). На исходном отрезке [a,b] выбираются две точки x1 и x2 , так, чтобы выполнялось приведенное выше соотношение «золотого сечения» этого отрезка. Вычисляются значения целевой функции в этих точках – 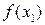 и
и 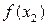 . Они сравниваются, и из дальнейшего рассмотрения исключается отрезок, прилегающий к точке, дающей большее значение целевой функции (здесь отрезок [x2,b] . Т.е. исходный отрезок [a, b] «стягивается» до отрезка [a, b1]. Для этого нового отрезка находится его середина, и по отношению к ней симметрично оставшейся точке x1 ставится точка x3. Для нее рассчитывается значение целевой функции
. Они сравниваются, и из дальнейшего рассмотрения исключается отрезок, прилегающий к точке, дающей большее значение целевой функции (здесь отрезок [x2,b] . Т.е. исходный отрезок [a, b] «стягивается» до отрезка [a, b1]. Для этого нового отрезка находится его середина, и по отношению к ней симметрично оставшейся точке x1 ставится точка x3. Для нее рассчитывается значение целевой функции 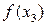 и сравнивается с
и сравнивается с 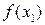 . Из дальнейшего рассмотрения опять исключается отрезок, прилегающий к точке с большим значением целевой функции, здесь это отрезок [a, x3]. Текущий отрезок «стягивается» до нового отрезка, здесь это [a1, b1] и т.д.
. Из дальнейшего рассмотрения опять исключается отрезок, прилегающий к точке с большим значением целевой функции, здесь это отрезок [a, x3]. Текущий отрезок «стягивается» до нового отрезка, здесь это [a1, b1] и т.д.
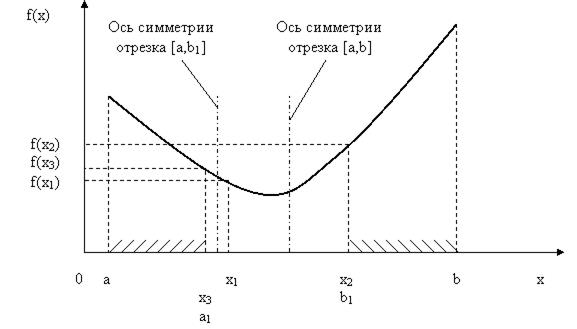
Рис. 5.7. Иллюстрация алгоритма метода «золотого сечения»
Метод «золотого сечения» прост, эффективен и широко применяется в практической оптимизации.
Метод парабол.
Методы, использующие исключение отрезков, основаны на сравнении функций в двух точках пробного отрезка, учитываются лишь значения функции в этих точках.
Учесть информацию о значениях функции между точками позволяют методы полиномиальной аппроксимации. Их основная идея заключена в том, что функция Φ(u) аппроксимируется полиномом, а точка его минимума служит приближением к u*. Разумеется, в этом случае кроме свойства унимодальности (т.е. наличия единственного минимума на рассматриваемом отрезке), необходимо на Φ(u) наложить и требования достаточной гладкости для ее полиномиальной аппроксимации.
Для повышения точности поиска u* можно как увеличивать степень полинома, так и уменьшать пробный отрезок. Поскольку первый прием приводит к заметному увеличению вычислительной работы и появлению дополнительных экстремумов, обычно пользуются полиномами второй (метод парабол) или третьей (метод кубической интерполяции) степени.
Алгоритм поиска минимума состоит в следующем.
Выбираем на пробном отрезке три точки u1, u2, u3 такие, что u1 < u2 < u3 и 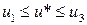 .
.
Построим параболу (квадратичный полином)
Q(u) = a0 + a1 (u - u1) + a2 (u - u1)(u - u2),
график которой проходит через точки (u1,f(u1)), (u2,f(u2)), (u3,f(u3)).
Коэффициенты ak, k = 1, 2, 3 находим из системы уравнений
Q(u1) = f(u1), Q(u2) = f(u2), Q(u3) = f(u3),
откуда
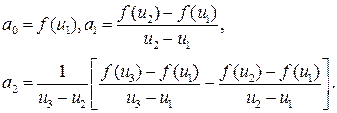
Точку 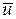 минимума Q(u) находим, приравнивания его производную к нулю:
минимума Q(u) находим, приравнивания его производную к нулю:
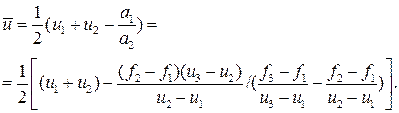
Далее полагаем: 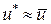 (очередное приближение точки минимума). Эту процедуру можно продолжить до достижения необходимой точности, выбирая новые точки uk, k = 1, 2, 3. Для этого можно использовать методы исключения отрезков, используя в качестве двух пробных точек u2 и
(очередное приближение точки минимума). Эту процедуру можно продолжить до достижения необходимой точности, выбирая новые точки uk, k = 1, 2, 3. Для этого можно использовать методы исключения отрезков, используя в качестве двух пробных точек u2 и 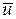 , таких, что u2,
, таких, что u2, 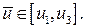
Дата добавления: 2017-01-26; просмотров: 3752;











