Метод наименьших квадратов
Одним из способов определения параметров эмпирической формулы является метод наименьших квадратов. В этом методе параметры a0, a1, ..., anопределяются из условия минимума суммы квадратов отклонений аппроксимирующей функции от табличных данных.
Вектор коэффициентов aT определяют из условия минимизации
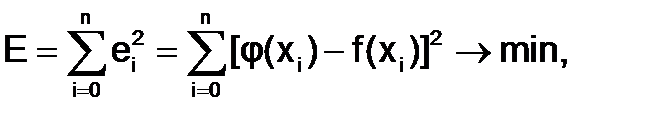
где (n+1) – количество узловых точек.
Условие минимума функцииЕ приводит к системе линейных уравнений относительно параметров a0, a1, ..., am. Эта система называется системой нормальных уравнений, её матрица – матрицаГрама. Элементамиматрицы Грамаявляются суммы скалярных произведений базисных функций
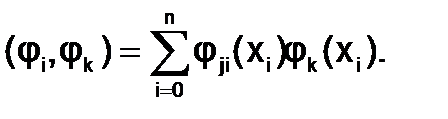
Для получения искомых значений параметров следует составить и решить систему (m+1) уравнения
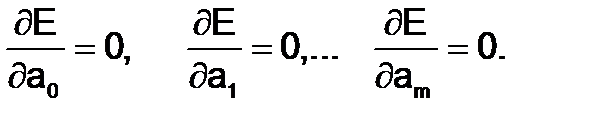
Пусть в качестве аппроксимирующей функции выбрана линейная зависимость y= a0+a1x . Тогда
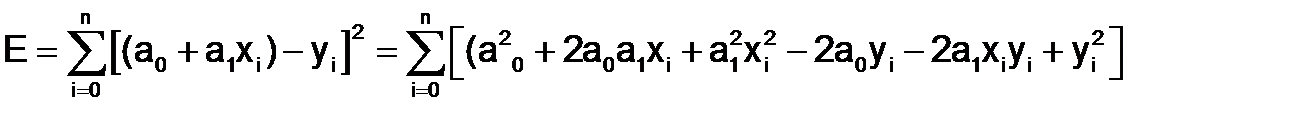 .
.
Условия минимума:
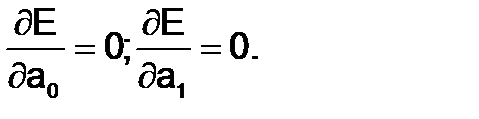
Тогда первое уравнение имеет вид
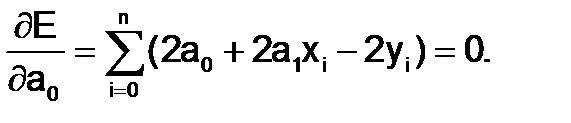
Раскрывая скобки и разделив на постоянный коэффициент, получим
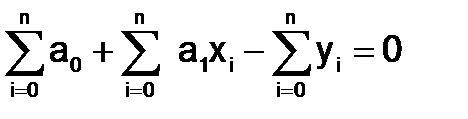 .
.
Первое уравнение принимает следующий окончательный вид:
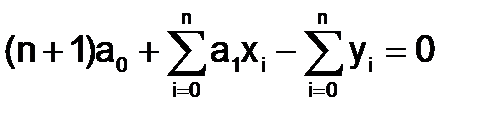 .
.
Для получения второго уравнения,приравняем нулю частную производную по а1:
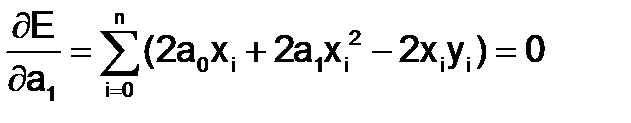 .
.
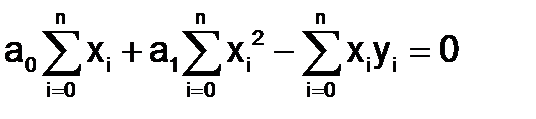 .
.
Система линейных уравнений для нахождения коэффициентов многочлена 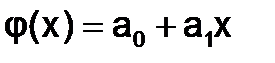 (линейная аппроксимация):
(линейная аппроксимация):
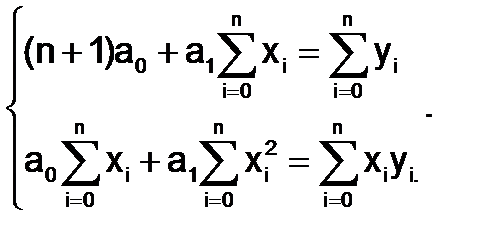
Введем следующие обозначения 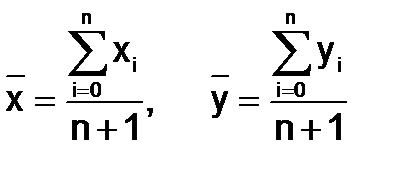 - средние значения исходных данных. Во введенных обозначениях решениями системы являются
- средние значения исходных данных. Во введенных обозначениях решениями системы являются
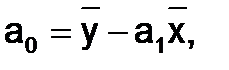
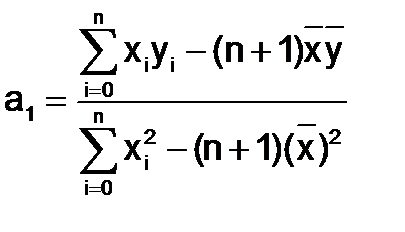 .
.
В случае применения метода наименьших квадратов для определения коэффициентов аппроксимирующего многочлена второй степени y=a0+a1x+а2х2 критерий минимизации имеет вид
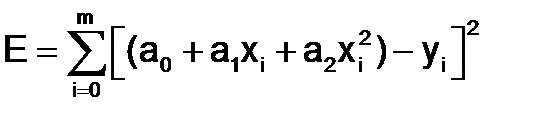 .
.
Из условия 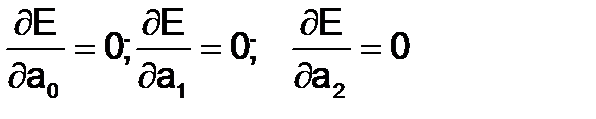 получим следующую систему уравнений:
получим следующую систему уравнений:
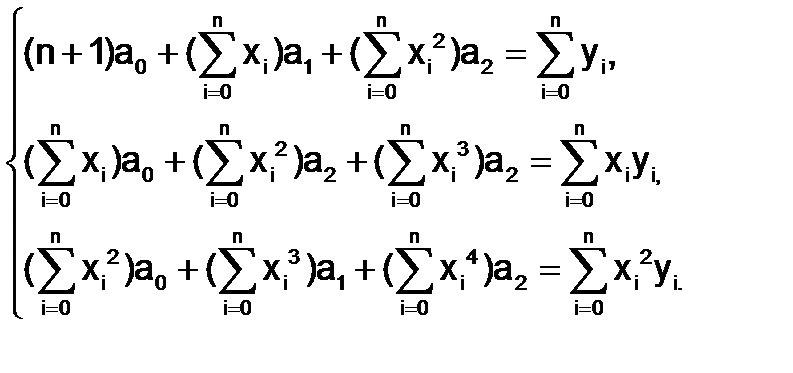
Решение этой системы уравнений относительно а0, а1, а2 позволяет найти коэффициенты эмпирической формулы 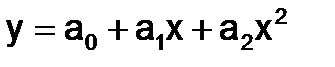 - аппроксимирующего многочлена 2-го порядка. При решении системы линейных уравнений могут быть применены численные методы.
- аппроксимирующего многочлена 2-го порядка. При решении системы линейных уравнений могут быть применены численные методы.
В случае степенного базиса (степень аппроксимирующего полинома равна m) матрица Грама системы нормальных уравнений G и столбец правых частей системы нормальных уравнений 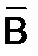 имеют вид
имеют вид
G = 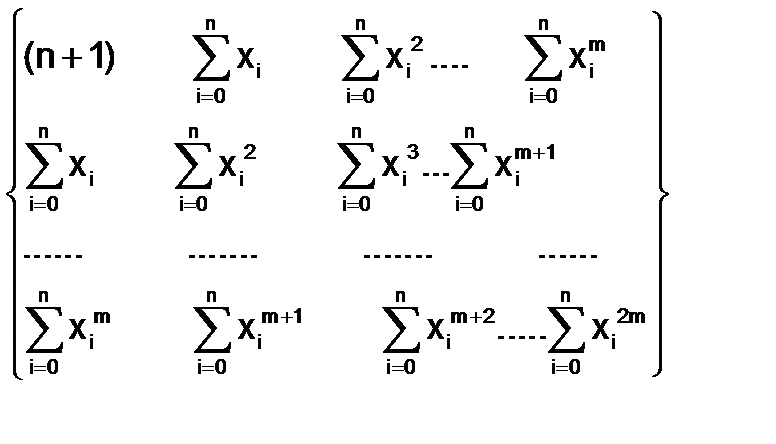
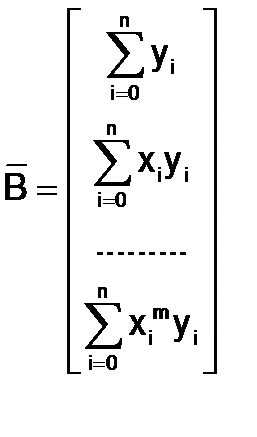
В матричной форме система нормальных уравнений примет вид:
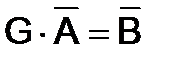 .
.
Решение системы нормальных уравнений
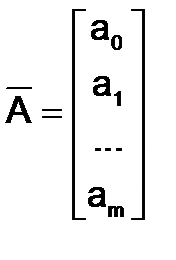
найдется из выражения 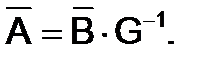
В качестве меры уклонения заданных значений функции y0, y1, ..., yn от многочлена степени m- φ(x)=a0 φ0(x)+a1 φ1(x)+...+amφm(x) ,принимается величина
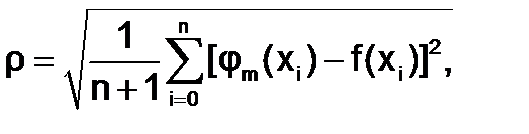
(n+1) – количество узлов, m – степень аппроксимирующего многочлена, n+1>=m.
На рис.1.7.2-1 приведена укрупненная схема алгоритма метода наименьших квадратов.
| |
Рис. 1.7.2-1. Укрупненная схема алгоритма метода наименьших квадратов
Данная схема алгоритма метода наименьших квадратов является укрупненной и отражает основные процессы метода, где n+1 – количество точек, в которых известны значения хi, yi; i=0,1,…, n.
Блок вычисления коэффициентов предполагает вычисление коэффициентов при неизвестных с0, с1, …, сm и свободных членов системы из m+1 линейных уравнений.
Следующий блок – блок решения системы уравнений – предполагает вычисление коэффициентов аппроксимирующей функциис0, с1, …, сm.
Далее вычисляется невязка
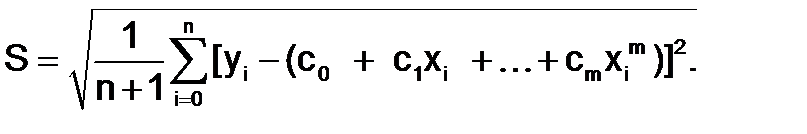
Дата добавления: 2016-05-31; просмотров: 2326;











