Метод конечных элементов

Среди численных методов решения наибольшее распространение получили метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Поскольку для решения связанных краевых задач ОМД в настоящее время широко используется МКЭ и имеются специализированные пакеты программ, то краткое рассмотрение и решение тепловых задач МКР будет рассмотрено на практических занятиях.

4.2.1. Понятие о методах конечных элементов

Метод конечных элементов (МКЭ) в настоящее время, пожалуй, самый распространенный в мире численный метод. К его достоинствам относятся:

- возможность счета на неравномерных сетках, в двумерном и трехмерном случаях для областей сложной геометрии;

- "технологичность" методов.

Основная идея метода конечных элементов, базирующая на методах Бубнова, Галеркина и Ритца, была предложена Р.Курантом в 1943 г., но осталась незамеченной, опередив потребности практики. В 50 - х годах прошлого века с появлением первых компьютеров возникла необходимость в разработке новых инженерных подходов к численному решению задач со сложной геометрией, в которых области интегрирования разбивались на подобласти. Такие подобласти (носители финитныхбазисных функций, об этом ниже) и получили название конечных элементов.

Метод конечных элементов основан на идее аппроксимации непрерывной функции φ^(е) (в физической интерпретации - температуры, давления, перемещения, скорости и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами [29, 30-32]. Исследуемая геометрическая область разбивается на элементы таким образом, чтобы на каждом из них неизвестная функция аппроксимировалась пробной функцией (как правило, полиномом). Причем эти пробные функции должны удовлетворять граничным условиям непрерывности, совпадающим с граничными условиями, налагаемыми самой задачей. Выбор для каждого элемента аппроксимирующей функции будет определять соответствующий тип элемента.

Будем рассматривать вычислительный алгоритм метода конечных элементов в формулировке, основанной на процедуре минимизации функционала, соответствующего решаемой непрерывной задаче. В результате выполнения указанной процедуры происходит замещение уравнения или системы уравнений в частных производных системой недифференциальных уравнений, имеющих в качестве коэффициентов аппроксимирующие функции, которые фактически являются значениями искомой функции в вершинах разбиения.

При решении задачи с помощью МКЭ необходимо определиться с формой конечного элемента.

Форма конечного элемента – его внешний вид, определяет точность аппроксимации границ исследуемого объекта

В одномерном случае выбор ограничен отрезком прямой. В двумерном случае форма конечного элемента может быть любой, при условии, что с помощью этого конечного элемента можно, с некоторой степенью точности аппроксимации границ, покрыть площадь произвольной формы (без перекрытия элементов). Наиболее простыми элементами для плоского случая являются треугольный и прямоугольный (со строронами, параллельными осям координат) элементы.

Для трехмерного случая форма элемента должны быть такой, чтобы с его помощью можно было бы покрыть объем произвольной формы, аппроксимировав при этом границы объекта. Наиболее простыми элементами являются тетраэдр и параллелепипед со стронами, параллельными осям координат. Условие параллельности упрощает вычисление локальных матрицы жесткости вектора нагрузок.

В общем случае алгоритм МКЭ состоит из четырех этапов:

Этап 1. Выделение конечных элементов (разбиение области на конечные элементы).

Этап 2. Определение аппроксимирующей функции для каждого элемента (определение функции элемента). На данном этапе значение непрерывной функции φ^(е) в произвольной точке е-го конечного элемента аппроксимируется полиномом

φ^(е)=А^(е)R + A₀, (4.8)

где А^(е) – вектор-строка коэффициентов полинома, A₀ – свободный член, R=(х,у,z) – вектор координат в рассматриваемой точке.

Задача этапа далее заключается в определении неизвестного вектора А^(е) и свободного члена A₀. Для этого, использя условие непрерывности функции в узлах, коэффициенты полинома выражают через вектор Ф^(е) узловых значений функции и координаты узлов и, проделав эквивалентные преобразования, получают

φ^(е)= N^(e)Ф^(е) , (4.9)

где N^(e) – матрица–сторка, элементы которой называют функциями формы конечного элемента.

Функции Фомы легко вычисляются через координаты самой точки и координаты узлов элементов.

Этап 3. Объединение конечных элементов в анасамбль. На этом этапе уравнения (4.9), относящиеся к отдельным элементам, объединяются в ансамбль, т.е. в систему алгебраических уравнений

φ = NФ. (4.10)

Система (4.10) является моделью искомой непрерывной функции.

Этап 4. Определение вектора узловых значений функции. В общем случае вектор Ф в (4.10) вначале неизвестен. Его определние – наиболее сложная процедура в МКЭ.

Оазработано несколько алгоритмов вычисления вектора Ф. Один из алгоритмов основан на минимизации функционала, связанного с физическим смыслом решаемой задачи, и состоит из следующих этапов:

Этап 1. Выбор функционала, зависящего для стационарных задач от искомой функции φ и её частных производных 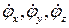по вектору пространственных координат

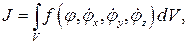
где V – объем.

Функционал J представляется суммой соответствующих функционалов, относящихся к отдельным конечным элементам

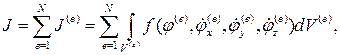(4.11)

где N – число элементов.

Этап 2. Подстановка аппроксимирующего выражения (4.9) в (4.11) и вычисление производных 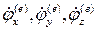по формулам вида

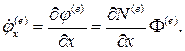
Этап 3. Минимизация по вектору Ф функционала J. Для этого составляяются уравнения

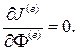(4.12)

Суммирование выражений (4.12) по конечным элементам приводит к системе алгебраических уравнений

КФ=F, (4.13)

где К – матрица коэффициентов – матрица жесткости, F – вектор нагрузки.

Матрица жесткости и вектор нагрузки представлят математическую модель в МКЭ.

Этап 4. Решение системы (4.13), позволяющее определить неизвестный вектор узловых значений.

Найденные значения вектора Ф подставляют в (4.10), после чего значение функции φ легко вычисляются в любой точке заданной области. Процедуру определения аппроксимирующей функции элементов выполняют один раз для типичного элемента области безотносительно к его топологическому положению в ней.

Представим, что заготовка в состоянии плоской деформации разделена на конечное число треугольных призматических элементов с воображаемыми границами (рис. 4.2). Элементы соединены только в узловых точках (узлах) и силы не могут передаваться через боковую поверхность элементов. Элементы и узлы так пронумерованы, что соседние элементы или узлы имеют близкие номера.

При небольшом перемещении инструмента узлы пермещаются в новые положения. Перемещения узлов считаются неизвестными параметрами, которые предстоит опрелеоить при заданных граничных условиях. В двумерной модели неизвестных параметров вдвое больше, чем узлов, поскольку каждому узлу соответствует две компоненты перемещения u вдоль оси x и v вдоль оси y. Приращения напряжений и деформаций могут быть определены в результате вычисления перемещений.

В качестве примера рассмотрим треугольный элнмент ijm в условиях плоской деформации (рис. 4.3).

Рис. 4.2. Разбивка на конечные элементы и индексация (нумерация) узлов и элементов

Рис. 4.3. Треугольный элемент с тремя узлами

Компоненты перемещения или скорости элемента интерполируются функцией перемещения. Простейшими функциями перемещения являются линейные полиномы

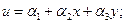(4.14а)

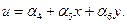(4.14б)

Коэффициенты α₁, α₂, …, α₆ определяются путем подстановки в эти уравнения перемещений и координат узловых точек, т.е.

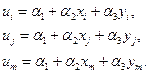(4.15)

Решение этих уравнений позволяет найти

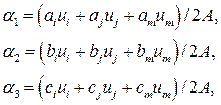(4.16)

где А – площадь треугольника ijm, т.е

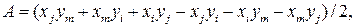
а a_i, b_i и c_i определены следующим выражением

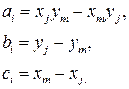
Другие коэффициенты получаются путем циклической перестановки индексов. Используя эти значения, уравнения (4.14) можно переписать в терминах скоростей узлов

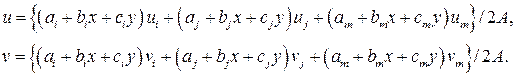(4.17)

Зависимости (4.17) можно представить в следующем виде

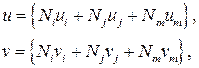(4.18)

или в матричном виде

,

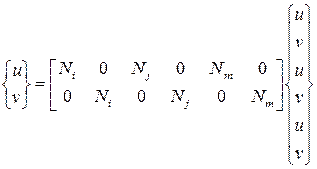где

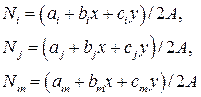
называют функциями формы элемента.

Рассмотрим процедуру составления ансамбля конечных элементов. В соответствии с рис. 4.2 начнем с узла 1 и ведем отсчет против часовой стрелки. Соответствие между этими обозначениями и глобальными номерами узлов следующее:

элемент 1 i = 1; j = 5; m =6;

элемент 2 i = 1; j = 6; m =2;

элемент 3 i = 2; j = 6; m =7;

элемент 4 i = 2; j = 7; m =3 и т.д.

Подставляя полученные значения в (4.18), получим

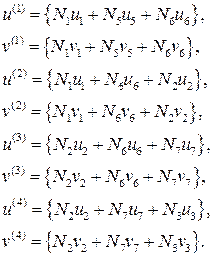
Данная система является моделью искомой непрерывной функции.

Матрица жесткости элемента в (4.13) находится из условия баланса работы внешних сил и суммарной внутренней работы [30-32] и имеет вид

,

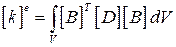где V – объем элемента, а матрица В определяется через производные от функций (4.17)и имеет вид

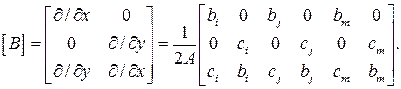
Матрица D вытекает из соотношения между напряжениями и деформациями σ = Dε и при плоском напряженном состоянии для условия пластичности Мизеса имеет вид

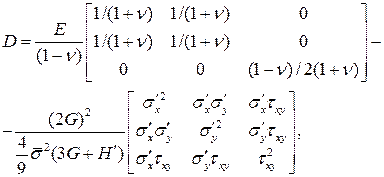
где Е – модуль упругости Юнга, v – коэффициент Пуассона, G = E/2(1+v) –модуль сдвига, 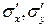– компоненты девиатора напряжений, 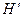– коэффициент упрочнения 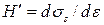, 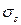– напряжение текучести.

Общая матрица жесткости для ансамбля элементов выразится в виде

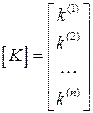
и будет представлять собой симметричную (в силу теоремы Бетти) матрицу. В итоге решение для (4.13) сведётся к решению системы уравнений с разряженной (ленточной)матрицей.

Мы рассмотрели только основы теории метода конечных элементов, для более глубокого изучения особенностей применения метода для решения задач ОМД необходимо обратиться к работам [29-32], а также уточнить эти вопросы при практическом освоении пакта ANSYS.

Пример решения одномерной задачи с помощью МКЭ.

Пусть необходимо найти удлинение балки, с одним закрепленным концом (рис. 4.4) с продольной нагружающей силой.

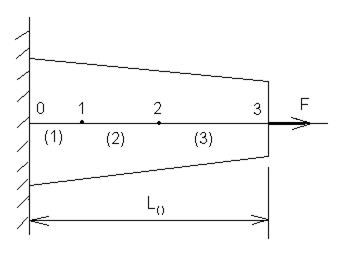
Рис. 4.4. Схема балки с одним закрепленным концом и продольной нагружающей силой

Уравнение, описывающее состояние балки имеет вид:

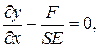
здесь y - удлинение, F - нагружающая сила, S - площадь поперечного сечения, E - модуль Юнга.

В соответствии с алгоритмом решения задач с помощью МКЭ:

1. Выбираем конечный элемент. Для одномерной задачи выбор ограничен только отрезком прямой.

2. Выбираем функцию формы конечного элемента, то есть фактически выбираем аппроксимацию решения внутри конечного элемента. Будем считать, что удлинение внутри конечного элемента меняется по линейному закону:

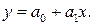(4.19)

Предполагаем, что нам известны узловые значения удлинений Y_i и Y_j (см. рис. 4.5).

Из (4.19) при 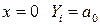, а при .

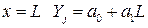Из данной системы уравнений находим значения 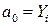и и 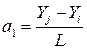подставляем в (4.19), выделяя коэффициенты пр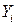и и :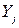

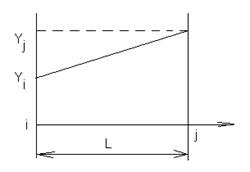
Рис. 4.5. Схема узловых значений удлинений

,

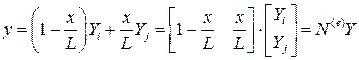где 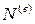- вектор функции формы конечного элемента, его составляющие элементы - глобальные базисные функции, отличные от нуля в пределах этого элемента.

3. Разбиваем область на конечные элементы.

4. Получение локальных матрицы жесткости и вектора нагрузок конечного элемента.

Локальная матрица жесткости и вектор нагрузок - математическая модель конечного элемента. Эти термины употребляются не только в задачах строительной механики, но и в других предметных областях

Фактически для их получения необходимо применить метод взвешенных невязок в пределах конечного элемента с аппроксимацией, полученной в в соответствии с методом Галеркина:

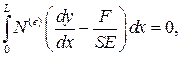
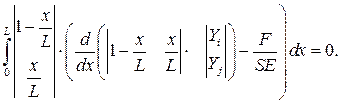
Раскрываем интеграл в предположении, что площадь поперечного сечения элемента постоянна:

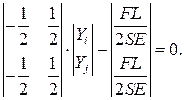
Приводим уравнение к следующему виду:

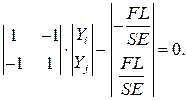(4.20)

Получили локальные матрицу жесткости и вектор нагрузок.

5. Ансамблирование.

Интеграл по одному конечному элементу мы вычислили в (4.20).

Глобальная матрица жесткости будет иметь размерность, определяемую числом узлов сетки, в нашем примере – 4. Вектор неизвестных составляют перемещения в этих узлах. Локальная матрица жесткости каждого конечного элемента даст аддитивный вклад в глобальную матрицу в соответствии с узлами подключения конечного элемента (это же касается и вектора нагрузок)

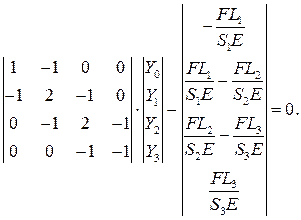
6. Учет граничных условий. В нашем примере 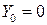, то есть можно вычеркнуть первый столбец и первую строку.

7. Решение системы уравнений

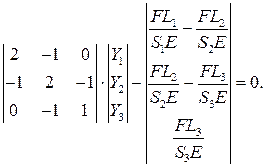
В результате найдем удлинение в каждом узле.