Аппроксимация по методу наименьших квадратов

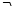Y Y(x) * * *   0 X

Пусть для некоторых значений аргумента "х_i" известны значения "y_i". Функция "Y", значения которой Y(x_i) можно использовать вместо "y_i", называется аппроксимирующей функцией. Как правило, аппроксимация применяется для получения функциональной зависимости, описывающей экспериментально полученные значения "y_i" при различных "х_i".

Рассмотрим разработанный Гауссом метод наименьших квадратов, при котором получается наилучшее приближение функции Y(x_i) к значениям y_i.

Метод заключается в аппроксимации "N" значений "y_i" полиномом степени "m":

Y(x) = A₀ + A₁ * x + A₂ * x² + . . . + A_m * x^m для которого сумма квадратов отклонений D_i = Y(x_i)-y_i минимальна. Коэффициенты A₀, A₁, A₂, . . . , A_m находятся при решении системы уравнений: ¶S/¶A₀=0; ¶S/¶A₁=0; ¶S/¶A₂=0; . . . ¶S/¶A_m=0;

где S = D₁² + D₂² + D₃² + . . . + D_N²;

В случае аппроксимации линейной функцией Y(x)= A₀ + A₁*x; для определения коэффициентов A₀ и A₁ необходимо решить систему двух уравнений:

N*A₀ + [X]*A₁ = [Y]; [X]*A₀ + [X²]*A₁ = [XY];

где [X]= x₁ + x₂ + x₃ + ... + x_N; [X²]= x₁² + x₂² + x₃² + ... + x_N²;

[Y]= y₁ + y₂ + y₃ + ... + y_N; [XY]= x₁*y₁+ x₂*y₂+ x₃*y₃+...+ x_N*y_N;

Решая систему, получаем:

A₀ = ([XY]*[X]-[Y]*[X²])/([X]*[X] - N *[X²]);

A₁ = ([X] *[Y]-[XY]*N) /([X]*[X] - N *[X²]);