Классификация технологических процессов и систем

Классификация необходима для установления математического строения описывающих ТП множеств и отображений.

ТП называется дискретным, если U={u_k: k=0, 1, ... , K}, причём T={t_k: k=0, 1, ... , K} при условии t_k-1< t_k и u_k(t_k). Для систем этого класса характерно Q={q(t_k) = g( t_k; u_k(t_k))} и Z ={z(t_k+t)=y(t_k+t;t_k, q(t_k))}.

ТП называется непрерывным, если U={u (t): t Î [0,T]}, T не аддитивно, а непрерывно, тогда Q={q(t) = g(t; t₀, u(t₀)} и Z = {z(t) = y(t; t₀, t, q(t, ×)}.

ТП называется стационарным, если 1) T является аддитивной группой; 2) для любого tÎ T из q(×) Î Q (×) следует 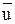(×) Î U(×), где для всех tÎT выполняется равенство 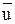(t – t) = u(t); 3) y(t; t₀, q(×)) = y(t – t; t₀ – t, 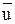(×)) для всех tÎT;

4) отображение j(t; t, z (×)) не зависит от t.

ТП называется нестационарным, если не выполнены условия стационарности.

ТП называется ограниченным первоначальной настройкой, если V = Æ,и полуограниченным, если в процессе функционирования отсутствует возможность управления размерами и формой области пластической деформации (например, процессы волочения, прессования, объемной штамповки и т.п.).

ТП называется (вполне) управляемым, если из любого состояния в данный момент времени его можно перевести в любое другое состояние под действием некоторого управления, т. е.

y (z', v) = z''

и разрешимо относительно v при любых z' и z''.

ТП называется наблюдаемым, если с формальной стороны восстановление начального состояния z по известным v и y сводится к решению уравнения y =j(z, v) относительно неизвестного z.

ТП называется настраиваемым (задача установочности), если при помощи фиксированного управления его можно перевести в фиксированное конечное состояние независимо от начального, т. е.

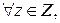y (z, v^*) = z^*,

состояние z^* называется установочным, а управление v^* – установочным управлением.

Важной проблемой анализа ТП является проблема устойчивости. Она возникает при изучении вопроса, будет ли ТП выполнять свою функцию и назначение в условиях, когда возникают различные возмущения, что часто является проявлением неполного знания об окружающей среде и самом процессе. Пусть назначение ТП состоит в преобразовании входа u⁰(×), который опосредованно через q(×) порождает процесс z⁰(×), в выход u^к(×)≡y⁰(·). Если в результате каких–то обстоятельств процесс z(×) в пространстве состояний не совпадает с z⁰(×), т. е. z^*(t₀) = z⁰(t₀) + Dz(t₀), что может быть следствием того, что в момент t₀ появилось отклонение Dz(t₀), то естественно возникает вопрос, сходится ли при t > t₀ и t ®¥ процесс y^*(t) = j(x⁰, t, z^* (t)) в некотором смысле к процессу y⁰(·) или будет близким к нему. Указанная сходимость будет иметь место, если j(x⁰, t, t₀, z⁰ + Dz, u⁰(·)) будет сходиться к j(x⁰, t, t₀, z⁰, u⁰(·)). Процесс z⁰(t) называется невозмущенным движением, а процесс z^* (×) – возмущенным движением. Изучение свойств отображения j, которые обеспечивают указанную сходимость процессов или их близость, составляет предмет теории устойчивости систем.