Выбор метода решения задачи

Поиск решения задачи сводится к отысканию некоторых зависимостей искомых величин от исходных параметров модели. Все методы решения можно подразделить на аналитические и алгоритмические.

Аналитические методы более удобны для пос­ледующего анализа результатов, но применимы лишь для относи­тельно простых моделей. В случае, если математическая задача (хотя бы и в упрощенной постановке) допускает аналитическое решение, последнее, без сомнения, предпочтительнее численного, что достаточно широко используется в теории обработки металлов давлением.

Алгоритмические методы сводятся к некоторому алгоритму, ре­ализующему вычислительный эксперимент с использованием ЭВМ. Точность моделирования в подобном эксперименте существенно за­висит от выбранного метода и его параметров (например, шага ин­тегрирования). Алгоритмические методы, как правило, более тру­доемки в реализации, требуют от исследователя хорошего знания методов вычислительной математики, обширной библиотеки специального программного обеспечения и мощной вычислитель­ной техники. Современные модели на базе алгоритмических мето­дов разрабатываются в исследовательских организациях, которые за­рекомендовали себя как авторитетные научные школы в соответ­ствующей области знания.

Приближенные и численные методы ис­следования поставленных математических задач относятся к обшир­ному разделу - современной вычислительной математике. Численные методы применимы лишь для корректных математических задач, что существенно ограничи­вает использование их в математическом моделировании.

Общим для всех численных методов является сведение мате­матической задачи к конечномерной [12]. Это чаще всего достига­ется дискретизацией исходной задачи, т.е. переходом от функции непрерывного аргумента к функциям дискретного аргумента.

Применение любого численного метода неминуемо приводит к погрешности результатов решения задачи. Выделяют три основ­ных составляющих возникающей погрешности при численном ре­шении исходной задачи [7]:

- неустранимая погрешность,связанная с неточным заданием
исходных данных (начальные и граничные условия, коэффи­циенты и правые части уравнений);

- погрешность метода,связанная с переходом к дискретному
аналогу исходной задачи (например, заменяя производную у'(х) разностным аналогом (у(х+∆х) - у(х))/∆х, получаем погрешность дискретизации, имеющую при ∆х → 0 порядок ∆х);

- ошибка округления,связанная с конечной разрядностью чи­сел, представляемых в ЭВМ.

Естественным требованием для конкретного вычислительного алгоритма является согласованность в порядках величин перечис­ленных трех видов погрешностей.

Численный, или приближенный, метод реализуется всегда в виде вычислительного алгоритма. Поэтому все требования, предъяв­ляемые к алгоритму, применимы и к вычислительному алгоритму. Прежде всего, алгоритм должен быть реализуем - обеспечивать решение задачи за допустимое машинное время. Важной характе­ристикой алгоритма является его точность, т.е. возможность по­лучения решения исходной задачи с заданной точностью ε > 0 за конечное число Q(ε)действий. Очевидно, чем меньше ε, тем боль­ше затрачиваемое машинное время. Для очень малых значений е время вычислений может быть недопустимо большим. Поэтому на практике добиваются некоторого компромисса между точностью и затрачиваемым машинным временем. Очевидно, что для каждой задачи, алгоритма и типа ЭВМ имеется свое характерное значение достигаемой точности.

Время работы алгоритма зависит от числа действий Q(ε), не­обходимых для достижения заданной точности. Для любой мате­матической задачи, как правило, можно предложить несколько алгоритмов, позволяющих получить решение с заданной точностью, но за разное число действий Q(ε). Алгоритмы, включающие мень­шее число действий для достижения одинаковой точности, будем называть более экономичными,или более эффективными.

В процессе работы вычислительного алгоритма на каждом акте вычислений возникает некоторая погрешность. При этом от дей­ствия к действию она может возрастать или не возрастать (а в не­которых случаях даже уменьшаться). Если погрешность в процессе вычислений неограниченно возрастает, то такой алгоритм называ­ется неустойчивым, или расходящимся. В противном случае алгоритм называется устойчивым, или сходящимся.

Выше уже отмечалось, что вычислительная математика объе­диняет огромный пласт разнообразных, быстро развивающихся чис­ленных и приближенных методов, поэтому практически невозмож­но привести их законченную классификацию. Стремление получить более точные, эффективные и устойчивые вычислительные алгорит­мы приводит к появлению многочисленных модификаций, учиты­вающих специфические особенности конкретной математической задачи или даже особенности моделируемых объектов.

Можно выделить следующие группы численных методов [12] по объектам, к которым они применяются:

- интерполяция и численное дифференцирование;

- численное интегрирование;

- определение корней линейных и нелинейных уравнений;

- решение систем линейных уравнений (подразделяют на пря­мые и итерационные методы);

- решение систем нелинейных уравнений;

- решение задачи Коши для обыкновенных дифференциальных уравнений;

- решение краевых задач для обыкновенных дифференциальных уравнений;

- решение уравнений в частных производных;

- решение интегральных уравнений.

Указанные численные методы далее будут рассмотрены более подробно.

Пример. Математическая постановка задачи моделирования уширения при кузнечной протяжке [13, 15].

Для получения решения сформулированной выше задачи (2.3) – (2.6) можно использовать как аналитические, так и численные методы.

Аналитическое решение представлено в работах [13,15].

Граничные условия (2.5) и (2.6) будут удовлетворены, если распределение скоростей описывается частным решением условия несжимаемости (2.4), а именно

v_x = C₁x + C₂,

v_y = C₃y + C₄,

v_z = – (C₁ + C₃)z + C₅,

где С₁, С₂, … , С₅ – постоянные интегрирования.

Принимая по обоснованию работы [15] C₂= C₄= C₅ = 0, а C₁ + C₃= v/h получим

v_x= C₁x,

v_y = C₃y

v_z = – (C₁ + C₃)z.

В дальнейшем вводят замену (2.2) [15]

φ = .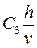

После замены кинематически возможные скорости в полосе и соответствующие им интенсивности скоростей деформаций определятся следующим образом:

для блока 1

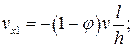
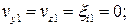
для блока 2

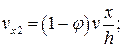
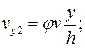
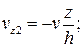
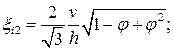
для блока 3

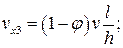
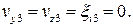
Сечения поковки x = ± l являются поверхностями разрывов скоростей (см. рис. 2.9). Эти разрывы: |Δv|₁₂ на стыке блоков 1 и 2, |Δv|₂₃ на стыке блоков 2 и 3 при одних и тех же координатах y и z, а x = ± l одинаковы

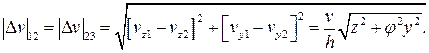
Скорости скольжения по поверхностям контакта при z = ±h распределяются симметрично

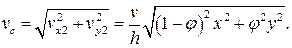
В результате составляющие уравнения мощностей всех сил (2.3) на указанных выше кинематически возможных скоростях

N_p = 2Pv, (2.7)

где P – сила деформации, действующая на боек;

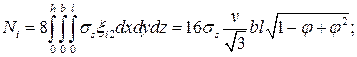(2.8а)

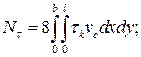(2.8б)

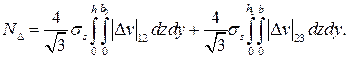(2.8в)

Приравнивая мощность внешних сил (2.7) к сумме мощностей деформации (2.8а), трения (2.8б) и на поверхностях разрыва (2.8в) получим выражение для силы протяжки

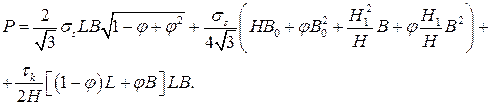(2.9)

Полученное уравнение содержит неизвестный параметр φ, который найдем из необходимого условия минимума верхней оценки силы протяжки (2.9)

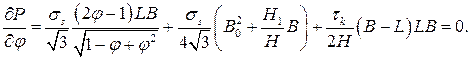
Из приведенного условия минимума силы Р следует

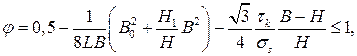(2.10)

где В₀ – начальная ширина полосы, Н₁ – конечная высота ее ранее протянутого участка, В, L,Н – текущие значения ширины полосы, длины площадки контакта (шаг подачи) и расстояние между бойками в очаге деформации.

В работе [18] приведено решение для аналогичной задачи при максимальном напряжении трения τ_к = σ_s/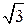

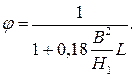(2.11)