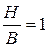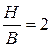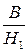Проверка адекватности моделей

Под адекватностьюматематической модели понимают степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.

Проверка адекватности модели преследует две цели:

1) убедиться в справедливости совокупности гипотез, сформу­лированных на этапах концептуальной и математической постановок. Переходить к проверке гипотез следует лишь после проверки использованных методов решения, комплексной отладки и устранения всех ошибок и конфликтов, связанных с программным обес­печением;

2) установить, что точность полученных результатов соответствует точности, оговоренной в техническом задании.

Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хо­рошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором - о сравне­нии с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требо­ваний, предъявляемых к модели, и ее назначения. При этом долж­на учитываться точность получения экспериментальных результа­тов или особенности постановок тестовых задач. В моделях, пред­назначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается точность 10—15%. В моделях, исполь­зуемых в управляющих и контролирующих системах, требуемая точность может быть 1–2% и даже более.

Пример.Проверка адекватностизадачи моделирования уширения при кузнечной протяжке.

Проверка разработанной математической модели (2.10) выполняется путем сравнения с имеющимися экспериментальными данными [15] (рис. 2.10), коэффициент корреляции 0,87-0,95.

Как следует из приведенных данных, расчетные значения достаточно хорошо описывают данные экспериментов, что может служить подтверждением адекватности модели.

Для модели (2.11) также на рис. 2.11 приведено сопоставление расчетных и экспериментальных данных [18], коэффициент корреляции 0,8.

φ

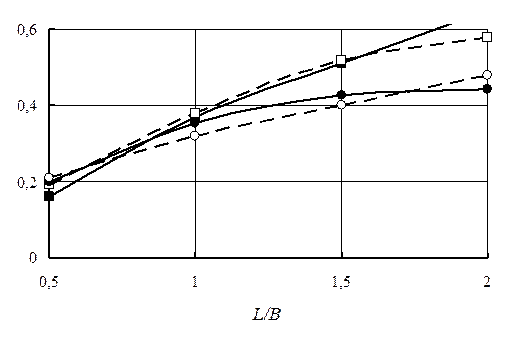
Рис. 2.10. Коэффициент уширения при протяжке полосы плоскими бойками:

– по расчетным данным; – по опытным данным

φ

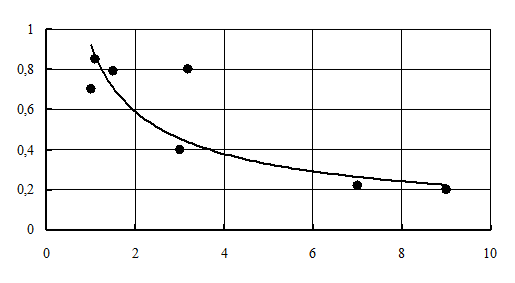
Рис. 2.11. Коэффициент уширения при протяжке полосы плоскими бойками:

– по расчетным данным; – по опытным данным А.П. Чекмарева