Математическая постановка задачи моделирования

Законченная концептуальная постановка позволяет сформули­ровать математическую постановку задачи моделирования, вклю­чающую совокупность различных математических соотношений, описывающих поведение и свойства объекта моделирования.

Математическая постановка задачи моделирования - это сово­купность математических соотношений, описывающих поведение и свойства объекта моделирования [7].

Как было отмечено в п. 2.1, совокупность математических со­отношений определяет вид оператора модели. Наиболее простым будет оператор модели в случае, если он представлен системой ал­гебраических уравнений. Подобные модели можно назвать моде­лями аппроксимационного типа, так как для их получения часто используют различные методы аппроксимации имеющихся экспе­риментальных данных о поведении выходных параметров объекта моделирования в зависимости от входных параметров и воздей­ствий внешней среды, а также от значений внутренних парамет­ров объекта.

Однако область применения моделей подобного типа ограни­чена. Для создания математических моделей сложных систем и про­цессов, применимых для широкого класса реальных задач требует­ся, как уже отмечалось выше, привлечение большого объема зна­ний, накопленных в рассматриваемой дисциплине (а в некоторых случаях и в смежных областях). В большинстве дисциплин (особен­но естественно-научных) эти знания сконцентрированы в аксио­мах, законах, теоремах, имеющих четкую математическую форму­лировку.

Следует отметить, что в обработке металлов давлением, основывающейся на механике сплошных сред, физике, технической механике принято выделять законы, справедливые для всех объектов исследования данной области знаний, и соотно­шения, описывающие поведение отдельных объектов или их сово­купностей. К числу первых в физике и механике относятся, напри­мер, уравнения баланса массы, количества движения, энергии и т.д., справедливые при определенных условиях для любых материаль­ных тел, независимо от их конкретного строения, структуры, со­стояния, химического состава. Уравнения этого класса подтверж­дены огромным количеством экспериментов, хорошо изучены и в силу этого применяются в соответствующих математических моде­лях как данность. Соотношения второго класса в физике и механи­ке называют определяющими,или физическимиуравнениями, или уравнениями состояния.Они устанавливают особенности поведения материальных объектов или их совокупностей (например, упругих или пластических сред) при воздействи­ях различных внешних факторов.

В качестве классических примеров определяющих соотношений можно привести закон Гука в теории упругости или условие пластичности Мизеса.

Соотношения второго класса гораздо менее изучены, а в ряде случаев их приходится устанавливать самому исследователю (осо­бенно при анализе объектов, состоящих из новых материалов). Не­обходимо отметить, что определяющие соотношения - это основ­ной элемент, «сердцевина» любой математической модели физико-механических процессов. Именно ошибки в выборе или установлении определяющих соотношений приводят к количественно (а в некоторых случаях и качественно) неверным результатам мо­делирования.

Совокупность математических соотношений указанных двух классов определяет оператор модели. В большинстве случаев опе­ратор модели включает в себя систему обыкновенных дифферен­циальных уравнений (ОДУ), дифференциальных уравнений в час­тных производных (ДУЧП) и/или интегродифференциальных урав­нений (ИДУ). Для обеспечения корректности постановки задачи к системе ОДУ или ДУЧП добавляются начальные или граничные условия, которые, в свою очередь, могут быть алгебраическими или дифференциальными соотношениями различного порядка.

Выделим несколько наиболее распространенных типов задач для систем ОДУ или ДУЧП:

- задача Коши, или задача с начальными условиями, в которой
по заданным в начальный момент времени переменным (на­чальным условиям) определяются значения этих искомых переменных для любого момента времени;

- начально-граничная, или краевая, задача,когда условия на ис­комую функцию выходного параметра задаются в начальный момент времени для всей пространственной области и на границе последней в каждый момент времени (на исследуемом интервале);

- задачи на собственные значения,в формулировку которых вхо­дят неопределенные параметры, определяемые из условия качественного изменения поведения системы (например, потеря устойчивости состояния равновесия или стационарно­го движения, появление периодического режима, резонанс и т.д.).

Для контроля правильности полученной системы математичес­ких соотношений требуется проведение ряда обязательных прове­рок [7].

Контроль размерностей, включающий правило, согласно которому приравниваться и складываться могут только величины одинаковой размерности. При переходе к вычислениям данная проверка сочетается с контролем использования
одной и той же системы единиц для значений всех параметров.

Контроль порядков,состоящий из грубой оценки сравнитель­ных порядков складываемых величин и исключением мало­значимых параметров. Например, если для выражения x + y + z=0 в результате оценки установлено, что в рассматриваемой области значений параметров модели |z| << |х| и |z| << y, то третьим слагаемым в исходном выражении мож­но пренебречь.

Контроль характера зависимостей заключается в проверке того, что направление и скорость изменения выходных параметров модели, вытекающие из выписанных математических соотношений, такие, как это следует непосредственно из «физического» смысла изучаемой модели.

Контроль экстремальных ситуаций- проверка того, какой вид принимают математические соотношения, а также результаты моделирования, если параметры модели или их комби­нации приближаются к предельно допустимым для них зна­чениям, чаще всего к нулю или бесконечности. В подобных экстремальных ситуациях модель часто упрощается, математические соотношения приобретают более наглядный смысл, упрощается их проверка. Например, в задачах механики деформируемого твердого тела деформация материала в исследуемой области в изотермических условиях возможна лишь при приложении нагрузок, отсутствие же нагрузок должно приводить к отсутствию деформаций.

Контроль граничных условий,включающий проверку того, что граничные условия действительно наложены, что они ис­пользованы в процессе построения искомого решения и что значения выходных параметров модели на самом деле удовлетворяют данным условиям.

Контроль физического смысла- проверка физического или иного, в зависимости от характера задачи, смысла исходных и промежуточных соотношений, появляющихся по мере кон­струирования модели.

Контроль математической замкнутости,состоящий в про­верке того, что выписанная система математических соотношений дает возможность, притом однозначно, решить по­ставленную математическую задачу. Например, если задача
свелась к отысканию п неизвестных из некоторой системы алгебраических или трансцендентных уравнений, то контроль замкнутости состоит в проверке того факта, что число независимых уравнений должно быть п. Если их меньше п, то надо установить недостающие уравнения, а если их больше п, то либо уравнения зависимы, либо при их составлении допущена ошибка. Однако если уравнения получаются из эксперимента или в результате наблюдений, то возможна постановка задачи, при которой число уравнений превыша­ет п, но сами уравнения удовлетворяются лишь приближен­но, а решение ищется, например, по методу наименьших квадратов. Неравенств среди условий также может быть лю­бое число, как это бывает, например, в задачах линейного программирования. Свойство математической замкнутости системы математичес­ких соотношений тесно связано с введенным Ж. Адамаром поня­тием корректно поставленной математической задачи [93], т.е. за­дачи, для которой решение существует, оно единственно и непре­рывнозависит от исходных данных. В данном случае решение считается непрерывным, если малому изменению исходных данных соответствует достаточно малое изменение решения.

Понятие корректности задачи имеет большое значение в при­кладной математике. Например, численные методы решения оправ­дано применять лишь к корректно поставленным задачам. При этом далеко не все задачи, возникающие на практике, можно считать корректными (например, так называемые обратные задачи). Дока­зательство корректности конкретной математической задачи - до­статочно сложная проблема, она решена только для некоторого класса математически поставленных задач. Проверка математичес­кой замкнутости является менее сложной по сравнению с провер­кой корректности математической постановки. В настоящее время активно исследуются свойства некорректных задач, разрабатывают­ся методы их решения. Аналогично понятию «корректно поставлен­ная задача» можно ввести понятие «корректная математическая модель».

Математическая модель является корректной,если для нее осу­ществлен и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстре­мальных ситуаций, граничных условий, физического смысла и ма­тематической замкнутости.

Пример. Математическая постановка задачи моделирования уширения при кузнечной протяжке [13, 15].

Для математического описания задачи составим схему протяжки полосы плоскими бойками (рис. 2.9).

Рис. 2.9. Схема протяжки полосы плоскими бойками

Кинематически возможная модель протяжки полосы представляет её состоящей из трех областей – блоков: внешних жестких 1 и 3 и центрального блока 2 (рис. 2.9), ограниченного координатными поверхностями x=±l, y=±b и z=±h, где распределение скоростей непрерывно.

Уширение зависит от отношения потока металла, проходящего через боковые грани полосы в очаге деформации

Q_y = 2|v_y|_y=b LH

к общему потоку металла, перемещаемого бойками

Q =2vLB,

что можно выразить через показатель уширения

φ = 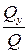. (2.2)

По смыслу задачи φ ограничена 0 < φ < 1.

Задача ставится следующим образом: найти такие функциональные зависимости скоростей, при которых полная энергия деформации

I = N_p + N_i + N_Δ + N_τ → min, (2.3)

принимает минимальное значение.

При этом должно выполняться условие несжимаемости

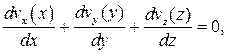(2.4)

а скорости в блоке 2 должны удовлетворять кинематическим граничным условиям

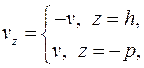(2.5)

где v – скорость бойков относительно срединного сечения полосы z = 0, а также удовлетворять условиям непрерывности нормальных составляющих скоростей в плоскостях симметрии и на плоских границах блока 2 с блоками 1 и 3:

v_x = 0 при x = 0; v_x=const при x = ±l; (2.6а)

v_y= 0 при y = 0; v_z = 0 при z = 0. (2.6б)