Равновесие зарядов на проводнике

В рамках электростатики мы рассматриваем задачи, в которых распределение зарядов отличается статичностью. Другими словами, такие состояния тел, которые реализуются после того, когда тела рассматриваемых систем пришли в равновесие после некоторых воздействий, например, сообщения заряда, помещения в электрическое поле и т.п. Проводники, в отличие от, диэлектриков, имеют в своем составе свободные носители заряда, которые могут перемещаться по объему проводника. В случае металлов такими носителями заряда являются электроны. Скорость их перемещения по металлу весьма высока, поэтому металлы приходят в равновесие в очень малые доли секунды. В случае других материалов может оказаться, что переход в равновесие происходит гораздо медленнее, однако мы сейчас будем рассматривать ситуации, когда равновесие достигнуто.

В состоянии равновесия выполняются следующие условия:

1.Напряженность поля внутри проводника была равна нулю: .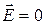

2.На поверхности (вблизи, в непосредственной окрестности…) проводника напряженность электрического поля перпендикулярна поверхности.

Эти условия являются следствиями наличия в проводнике свободных носителей заряда. Действительно, в равновесии перемещение зарядов должно отсутствовать, а, значит, напряженность поля внутри проводника должна быть равна нулю. Следствием этого условия является утверждение о том, что все точки проводника должны иметь одинаковый потенциал, и поверхность проводника является эквипотенциальной.

Поскольку внутри проводника в равновесии не может быть некомпенсированных зарядов (они создавали бы ненулевое поле внутри проводника), то заряд сообщаемый проводнику, располагается в очень тонком слое проводника вблизи поверхности, т.е. на поверхности проводника.

На поверхности проводника у вектора напряженности электрического поля должна отсутствовать тангенциальная (направленная по касательной к поверхности составляющая) составляющая. При ее наличии должно было бы происходить движение зарядов вдоль поверхности, чего в равновесии не может быть. Это утверждение справедливо для любого направления, поэтому вектор напряженностидолжен быть перпендикулярен поверхности.

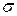Заряд, сообщенный проводнику, располагается на его поверхности с плотностью . Поток вектора электрической индукции 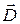через поверхность цилиндра, показанного на рисунке 16.1, по теореме Гаусса должен быть равен величине свободного заряда, заключенного внутри поверхности – 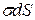. Однако поток через боковую поверхность отсутствует, поскольку вектор напряженности (а значит и вектор индукции) параллелен ей, поток через основание внутри проводника отсутствует – там нет электрического поля, а поток через внешнее основание равен 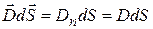. Поэтому

,

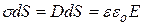
и напряженность электрического поля вблизи поверхности проводника определяется соотношением:

(16.1)

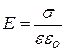
Представим уединенный проводник которому сообщен некоторый заряд. На большом, по сравнению с размерами проводника, расстоянии от него, независимо от формы проводника, его можно считать точечным заряженным телом. Эквипотенциальные поверхности точечного заряда являются сферами. Вблизи проводника эквипотенциальные поверхности должны приблизительно повторять его форму. Вследствие этого вблизи концов проводника эквипотенциальные поверхности сгущаются. Это означает, что потенциал в этих точках пространства изменяется быстро, а напряженность поля, соответственно достигает больших значений. Вследствие большой напряженности поля вблизи острых концов проводников возможно возникновение газового разряда, сопровождающегося стеканием заряда с проводника. По этой причиной элементы высоковольтных линий электропередач обязательно выполняются с округлыми поверхностями.

При помещении проводника во внешнее поле свободные заряды проводника смещаются до тех пор, пока не будут выполнены условия равновесия. При этом на различных участках проводника возникают заряды, распределенные по его поверхности с некоторой плотностью так, чтобы выполнялись условия равновесия. Эти заряды называют индуцированными, а само явление их возникновения – электрической индукцией (не путать с вектором электрической индукции!).