Соотношения векторного анализа

<54 55 565758 59 60 >

При использовании оператора Ñ необходимо помнить, что он является векторным и дифференциальным одновременно и действует на функции, записанные непосредственно после него.

Градиент произведения скалярных функций 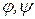по правилам дифференцирования:

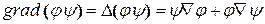. (13.45)

Аналогично дивергенция произведения скалярной функции 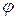на векторную 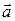по правилам дифференцирования:

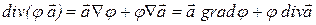. (13.46)

Поскольку градиент является векторной функцией, то от него можно взять дивергенцию. При этом необходимо учесть векторный характер оператора Гамильтона:

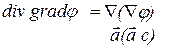. (13.47)

Считая Ñ вектором, преобразуем правую часть (13.46):

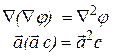. (13.48)

Поскольку квадрат оператора Гамильтона часто встречается в выражениях

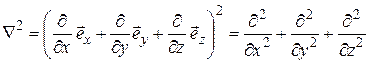его обозначают одним символом 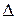и называют оператором ЛАПЛАСА.

Поэтому для дивергенции градиента скалярной функции можем записать:

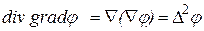. (13.49)

Дивергенция ротора 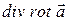с точки зрения векторного анализа представляет собой смешанное произведение векторов, в котором два вектора одинаковы. Геометрический смысл смешанного произведения – объем параллелепипеда, построенного на векторах. Но если в произведении два одинаковых вектора, то объем равен нулю! Поэтому

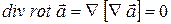. (13.50)

Соотношение (13.50) означает, что поле ротора не имеет источников. Поэтому можно утверждать, что если некоторое векторное поле можно представить в виде ротора векторной функции, то это поле не имеет источников. Именно поэтому поток 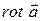через любую поверхность S, опирающуюся на данный контур Г всегда одинаков в соответствии с теоремой Стокса. Линии поля, представленного в виде ротора всегда замкнуты.

Применим операцию ротор к градиенту скалярной функции:

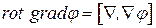. (13.51)

В векторном произведении в правой части (13.50) два одинаково направленных вектора. Поэтому оно равно нулю, а значит

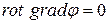. (13.52)

Формула (13.52)означает, что, если некоторое векторное поле можно представить в виде градиента скалярной функции, то ротор, а значит и циркуляция такого векторного поля равна нулю.

Результат применения операции ротор к ротору с точки зрения векторного анализа представляет собой двойное векторное произведение, которое раскрывается по правилу «bac-cab» :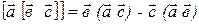

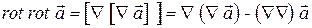. (13.53)

Поэтому

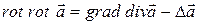. (13.54)

<54 55 565758 59 60 >

Дата добавления: 2017-01-26; просмотров: 2481;