УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
Уравнение состояния идеального газа удовлетворительно описывает поведение реальных газов только при не очень высоких давлениях и высоких температурах. Более точное описание в широком диапазоне давлений и температур дает уравнение Ван-дер-Ваальса, которое для одного моля имеет вид:
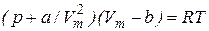 , (7.38)
, (7.38)
где 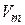 - объем моля;
- объем моля;
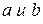 - экспериментально определяемые для каждого газа константы.
- экспериментально определяемые для каждого газа константы.
Очевидно, что уравнение (7.38) получено из уравнения для идеального газа путем введения поправок. Поправка 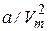 учитывает существование взаимного притяжения молекул газа. При этом взаимодействуют молекулы, находящиеся в пределах радиуса молекулярного действия. Вследствие этого притяжения давление внутри газа оказывается больше, чем оказываемое извне давление на величину, которую называют внутренним давлением. Сила взаимодействия элементарных объемов в пределах этого расстояния пропорциональна концентрации молекул в одном и другом объемах, а концентрация, в свою очередь обратно пропорциональна V. Соответственно, внутреннее давление также должно быть обратно пропорционально
учитывает существование взаимного притяжения молекул газа. При этом взаимодействуют молекулы, находящиеся в пределах радиуса молекулярного действия. Вследствие этого притяжения давление внутри газа оказывается больше, чем оказываемое извне давление на величину, которую называют внутренним давлением. Сила взаимодействия элементарных объемов в пределах этого расстояния пропорциональна концентрации молекул в одном и другом объемах, а концентрация, в свою очередь обратно пропорциональна V. Соответственно, внутреннее давление также должно быть обратно пропорционально 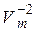 .
.
Поправка 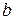 учитывает тот факт, что вследствие конечности объема каждой молекулы не весь объем сосуда V доступен для движения молекул. Количество она равна нескольким объемам молекул, содержащихся в моле газа.
учитывает тот факт, что вследствие конечности объема каждой молекулы не весь объем сосуда V доступен для движения молекул. Количество она равна нескольким объемам молекул, содержащихся в моле газа.
Поскольку в уравнении Ван-дер-Ваальса учитывается взаимодействие молекул на расстоянии, выражение для внутренней энергии вандерваальсовского газа должно включать энергию взаимодействия молекул. Работа расширения против сил внутреннего давления равна приращению энергии:
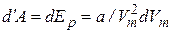 . (7.39)
. (7.39)
Интегрируя (31), находим:
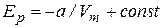 , (7.40)
, (7.40)
Тогда для внутренней энергии можно записать выражение:
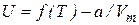 , (7.41)
, (7.41)
При 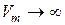 (7.41) должно переходить в выражение для внутренней энергии идеального газа, а значит
(7.41) должно переходить в выражение для внутренней энергии идеального газа, а значит 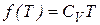 и
и
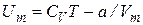 , (7.42)
, (7.42)
Дата добавления: 2017-01-26; просмотров: 1420;











