Обратная функция. Функция, заданная неявно и параметрически
Функция 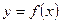 , где
, где 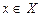 , называется обратимой на множестве
, называется обратимой на множестве 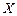 , если каждому значению у из множества значений функции
, если каждому значению у из множества значений функции 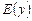 соответствует единственное значение
соответствует единственное значение 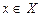 .
.
Если 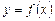 – обратимая функция, то на множестве У определена функция g, которая каждому значению
– обратимая функция, то на множестве У определена функция g, которая каждому значению 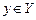 ставит в соответствие
ставит в соответствие 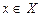 такое, что
такое, что 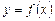 , т.е. определена
, т.е. определена 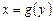 . Поэтому
. Поэтому 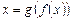 .
.
Функция g называется обратной функцией к f.
Функции f и g называются взаимно обратными функциями. Графики взаимно-обратных функций f и g симметричны относительно прямой 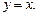
Если функции f и g взаимно обратны, то 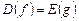 и
и 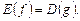
Для нахождения обратной функции из равенства 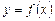 выражают х через у (если это возможно), а затем переобозначают переменные (через
выражают х через у (если это возможно), а затем переобозначают переменные (через 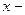 независимую переменную, через
независимую переменную, через 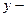 зависимую).
зависимую).
Пусть 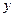 является функцией переменной
является функцией переменной 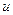 , а переменная
, а переменная 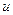 , в свою очередь, является функцией от переменной
, в свою очередь, является функцией от переменной 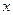 , т.е.
, т.е. 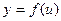 и
и 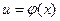 . Тогда функция
. Тогда функция 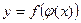 называется сложной функцией (или функцией от функции), если область определения функции
называется сложной функцией (или функцией от функции), если область определения функции 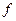 содержит множество значений функции
содержит множество значений функции 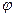 . Переменная
. Переменная 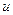 в этом случае называется промежуточной переменной.
в этом случае называется промежуточной переменной.
Всякую линию на координатной плоскости, которая не имеет разрывов, называют кривой линией.
График функции 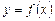 , который не имеет разрывов, является кривой линией. Однако не всякая кривая линия является графиком функции (график функции задается при условии, что каждому значению
, который не имеет разрывов, является кривой линией. Однако не всякая кривая линия является графиком функции (график функции задается при условии, что каждому значению 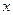 соответствует единственное значение
соответствует единственное значение 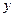 ).
).
Говорят, что функция 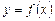 ,
, 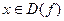 , задана неявно уравнением
, задана неявно уравнением
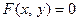 , (2)
, (2)
где 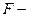 некоторое выражение от переменных
некоторое выражение от переменных 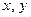 , при условии
, при условии
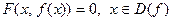 .
.
Функцию, заданную явно уравнением 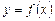 , можно привести к виду (2):
, можно привести к виду (2):
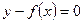 , (3)
, (3)
(в равенстве (3) 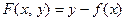 ). Однако, не всякую функцию, заданную неявно, можно задать в виде
). Однако, не всякую функцию, заданную неявно, можно задать в виде 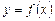 . Уравнение (2), не всегда однозначно разрешимо относительно переменной у или вообще не разрешимо. Оно задает часто кривую линию, но не график функции.
. Уравнение (2), не всегда однозначно разрешимо относительно переменной у или вообще не разрешимо. Оно задает часто кривую линию, но не график функции.
Для нахождения точки, лежащей на линии, которая задается уравнением (2), необходимо придать переменной 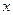 некоторое числовое значение, а затем из уравнения (2) найти соответствующее значение
некоторое числовое значение, а затем из уравнения (2) найти соответствующее значение 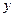 (возможно, несколько значений
(возможно, несколько значений 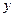 ). Для построения соответствующей кривой придают переменной
). Для построения соответствующей кривой придают переменной 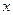 некоторое количество числовых значений, получим множество точек, принадлежащих искомой линии (2). Эти точки следует соединить непрерывной линией.
некоторое количество числовых значений, получим множество точек, принадлежащих искомой линии (2). Эти точки следует соединить непрерывной линией. 
Уравнения вида
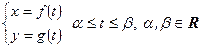 (4)
(4)
называют параметрическими уравнениями линии, где t – параметр или вспомогательная переменная, а 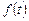 и
и 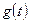 – функции параметра
– функции параметра 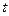 .
.
Каждому значению параметра t из заданного промежутка 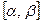 соответствует определенные значения х и у (вычисляемые по формулам (4)), которые и определяют положение точки
соответствует определенные значения х и у (вычисляемые по формулам (4)), которые и определяют положение точки 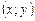 в системе координат
в системе координат 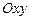 .
.
Для построения линии, заданной параметрическими уравнениями, выбирают достаточное количество значений  параметра
параметра 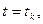 где
где 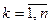 , вычисляют соответствующие значения
, вычисляют соответствующие значения 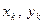 . Затем строятся точки
. Затем строятся точки 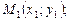
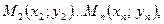 которые потом соединяются непрерывной линией.
которые потом соединяются непрерывной линией.
Чтобы от уравнений (4) перейти к уравнению типа 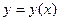 необходимо исключить параметр
необходимо исключить параметр 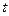 из уравнений системы (4).
из уравнений системы (4).
Пример 1.Найти функцию, обратную данной (если она существует) и построить графики данной функции и ей обратной в одной системе координат.
1) 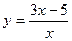 ; 2)
; 2) 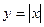 .
.
Решение. 1. Функция 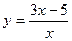 монотонна, поэтому для нее существует обратная функция. Выразим
монотонна, поэтому для нее существует обратная функция. Выразим 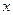 через
через 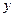 :
:
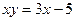 ,
, 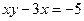 ,
, 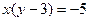 ,
,
т.е. 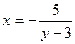 .
.
Обозначим независимую переменную через 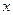 , а зависимую – через
, а зависимую – через 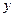 :
:
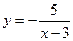 .
.
Обратная к заданной функции 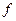 есть функция
есть функция 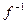 и она имеет вид:
и она имеет вид:
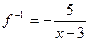 , где
, где 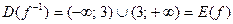 ,
,
а 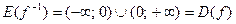 .
.
Строим графики функции 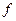 и
и 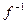 (рис.1)
(рис.1)
Рис. 1
2. Так как функция 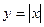 не является монотонной на промежутке
не является монотонной на промежутке 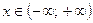 , то обратной функции
, то обратной функции 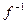 для нее не существует.
для нее не существует.
Пример 2. Из уравнения окружности 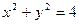 выразить явной
выразить явной 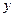 через
через 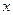 .
.
Решение. Из уравнения 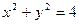 выразим
выразим 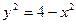 , откуда получаем совокупность двух функций
, откуда получаем совокупность двух функций 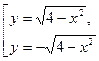
Графиком первого уравнения совокупности является полуокружность в верхней полуплоскости системы 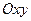 при условии, что
при условии, что 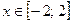 .
.
Графиком второго уравнения совокупности является полуокружности в нижней полуплоскости системы 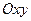 при условии, что
при условии, что 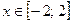 .
.
Пример 3. Построить кривую, заданную параметрически уравнениями
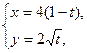
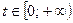 .
.
Решение. Для построения кривой выберем достаточное количество значений параметра 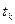 и вычислим соответствующие значения
и вычислим соответствующие значения 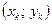 . Данные занесем в таблицу:
. Данные занесем в таблицу:
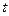
| 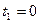
| 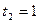
| 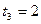
| 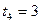
| 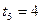
|
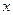
| 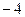
| 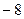
| 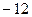
| ||
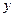
| 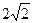
| 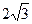
|
Построим точки 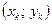 в системе координат
в системе координат 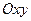 и соединим их плавной линией (рис.2).
и соединим их плавной линией (рис.2).
Рис.2
Задания
I уровень
1.1. Найдите функцию, обратную данной, если она существует.
1) 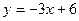 ; 2)
; 2) 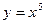 ; 3)
; 3) 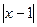 .
.
1.2. Докажите, что пары функций являются взаимно обратными.
1) 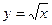 и
и 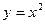 , если
, если 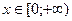 ;
;
2) 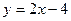 и
и 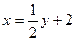 ;
;
3) 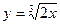 и
и 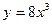 ;
;
4) 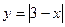 и
и 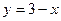 , если
, если 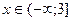 .
.
1.3. Постройте график функции и ей обратной (если она существует) в одной системе координат.
1) 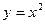 , если
, если 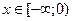 ; 2)
; 2) 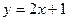 ;
;
3) 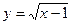 ; 4)
; 4) 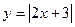 , если
, если 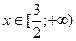 .
.
1.4. Найдите точку, принадлежащую кривой для заданного значения 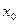 .
.
1) 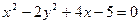 ,
, 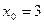 ;
;
2) 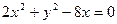 ,
, 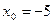 ;
;
3) 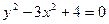 ,
, 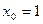 .
.
1.5. Запишите функцию в явном виде.
1) 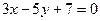 ; 2)
; 2) 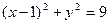 .
.
1.6. Найдите соответствующие точки кривой, заданной параметрически уравнениями, если заданы значения параметра 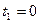 ;
; 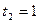 ;
; 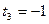 ;
; 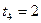 ;
; 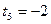 .
.
1) 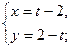 2)
2) 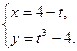
II уровень
2.1. Найдите функцию, обратную данной и постройте их графики в одной системе координат:
1) 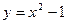 ; 2)
; 2) 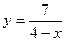 ;
;
3) 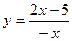 ; 4)
; 4) 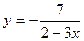 ;
;
5) 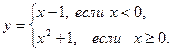
2.2. Определите, обратима ли функция
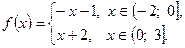
2.3. Найдите точки пересечения графиков 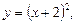 где
где 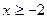 и обратной ей функции.
и обратной ей функции.
2.4. Пусть графиком функции является полуокружность с центром О(0; 0) и радиусом равным 5, расположенная в нижней координатной полуплоскости. Определите, существует ли функция, обратная данной.
2.5. Пусть задана функция 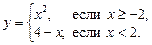 Найдите промежутки, на которых данная функция обратима.
Найдите промежутки, на которых данная функция обратима.
2.6. Выразите явно 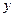 через
через 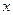 из уравнения и постройте данную линию:
из уравнения и постройте данную линию:
1) 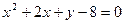 ; 2)
; 2) 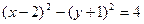 ;
;
3) 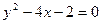 .
.
2.7. Постройте линию, заданную параметрически уравнениями:
1) 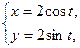
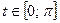 ; 2)
; 2) 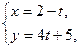
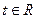 ;
;
3) 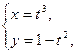
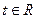 .
.
III уровень
3.1. Найдите функцию, обратную данной и постройте их графики в одной системе координат:
1) 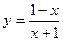 ; 2)
; 2) 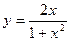 ;
;
3) 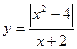 ; 4)
; 4) 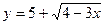
5) 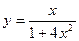 ,
, 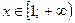 ; 6)
; 6) 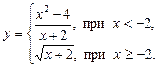
3.2. Докажите, что 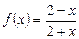 обратна сама себе.
обратна сама себе.
3.3. Найдите 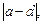 если
если 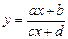 обратна к функции
обратна к функции 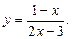
Дата добавления: 2016-07-27; просмотров: 4380;











