Основные методы интегрирования
К наиболее важным методам интегрирования относятся:
1) метод непосредственного интегрирования (с которым мы познакомились в предыдущей лекции);
2) метод замены переменной;
3) метод интегрирования по частям.
Метод замены переменной (или метод подстановки)
Этот метод основан на следующей теореме:
Теорема. Если F(x)- первообразная функции f(x), а 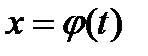 - дифференцируемая функция, то функция
- дифференцируемая функция, то функция 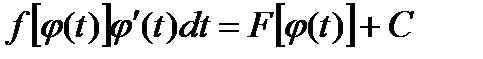 также имеет первообразную, причем
также имеет первообразную, причем
Поскольку 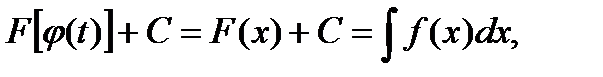
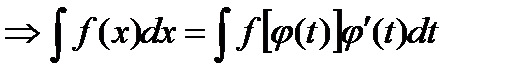 - формула замены переменной в неопределенном интеграле.
- формула замены переменной в неопределенном интеграле.
Таким образом, метод замены переменной состоит в следующем:
Пусть требуется вычислить 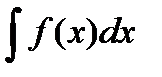 , причем непосредственно подобрать первообразную для функции
, причем непосредственно подобрать первообразную для функции 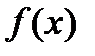 нельзя, но известно, что она существует.
нельзя, но известно, что она существует.
Введем в место х новую переменную t, положив 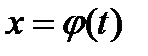 ,
,
где 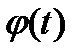 -дифференцируемая функция.
-дифференцируемая функция.
Тогда 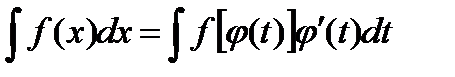
Допустим, что интеграл, стоящий в первой части равенства, легко находится:
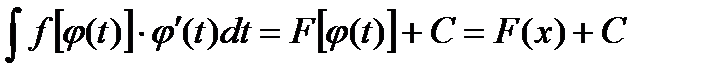
Итак, метод подстановок заключается в том, что в данном интеграле переменную х заменяют некоторой функцией 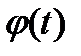 от новой переменной t.
от новой переменной t.
Это приводит к новому интегралу  , более простому при удачном выборе функции
, более простому при удачном выборе функции 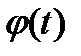 .
.
После его вычисления в полученном результате заменяют «t» через «x».
Этим самым будет найден интеграл 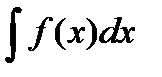 .
.
Пример6.6.13. 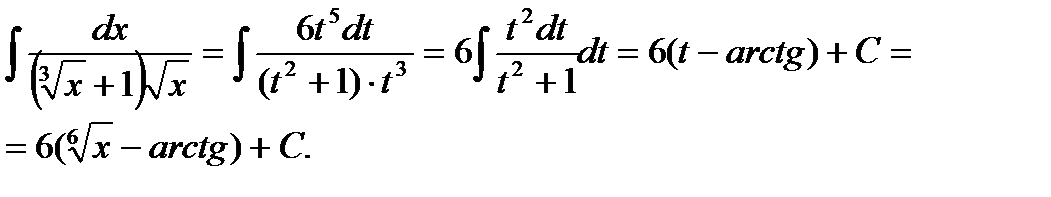
положим 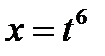 ,чтобы все корни извлекались
,чтобы все корни извлекались 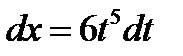 .
.
Пример 6.6.14. 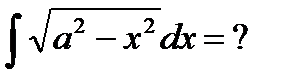
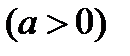
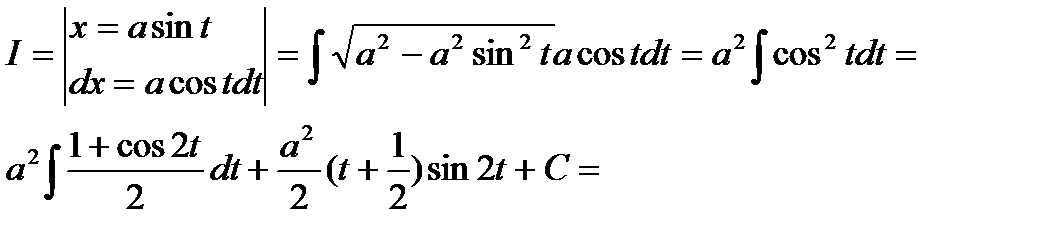
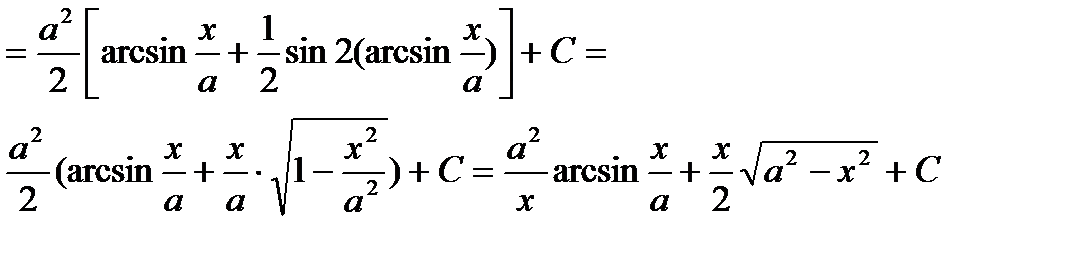 .
.
Обязательно возвращаться к исходной переменной х.
При замене переменной очень часто удобно бывает задавать не х как функцию от t, а, наоборот, задавать t как функцию от x и писать подстановку в виде 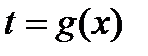
Теоретически оба эти способа равнозначны.
Рассмотрим ряд примеров на применение подстановки 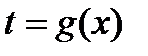 .
.
Пример 6.6.15. 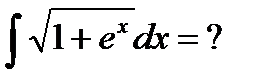
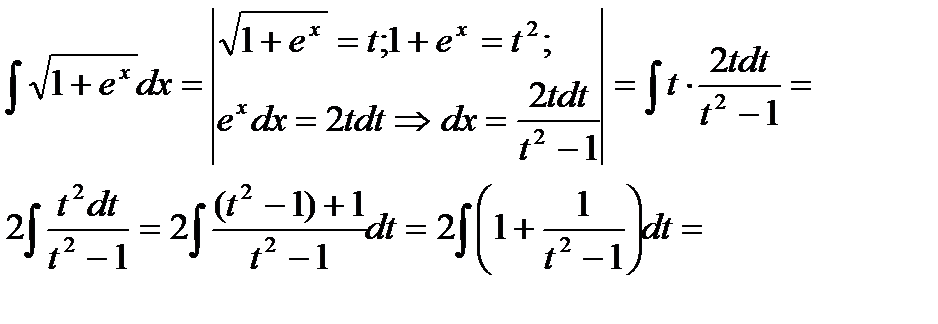
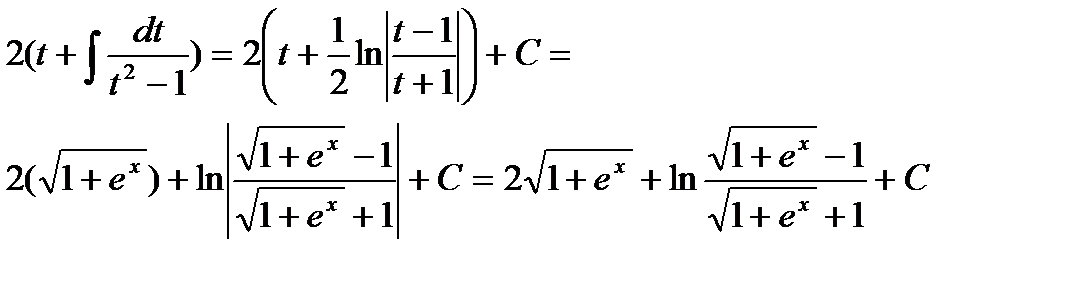 .
.
Пример 6.6.16. 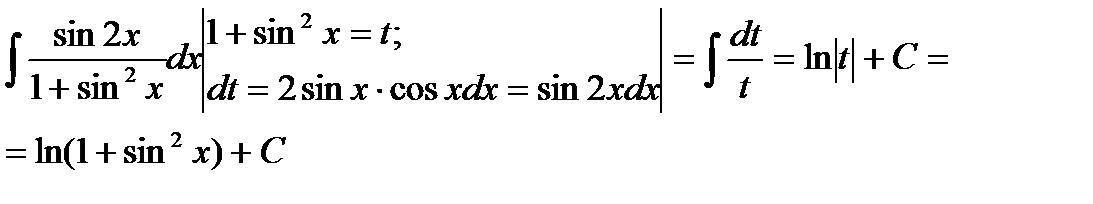 .
.
Пример 6.6.17. 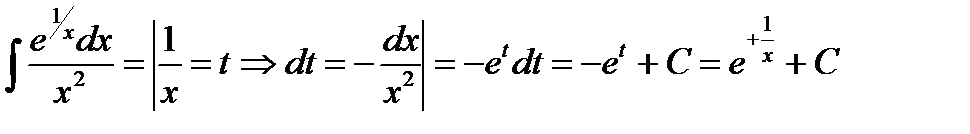 .
.
В последних двух примерах иногда интегрирование целесообразно выполнять без формального введения новой переменной (новой буквы) – применить способ подведения под знак дифференциала.
Доказано, по определению дифференциала функции, 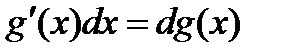 .Переход в этом равенстве слева направо называют «подведением множителя
.Переход в этом равенстве слева направо называют «подведением множителя 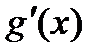 под знак дифференциала».
под знак дифференциала».
Если под интегральное выражение может быть разбито на 2 множителя, один из которых есть дифференциал некоторой функции 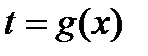 , а другой представляет собой легко интегрируемую функцию от t:
, а другой представляет собой легко интегрируемую функцию от t:
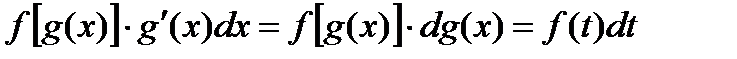 , то целесообразно подстановку
, то целесообразно подстановку 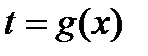 производить устно, в уме, это освобождает от излишней записи и ускоряет операцию интегрирования.
производить устно, в уме, это освобождает от излишней записи и ускоряет операцию интегрирования.
Так, в рассмотренных выше примерах это будет выглядеть таким образом.
Пример6.6.18. 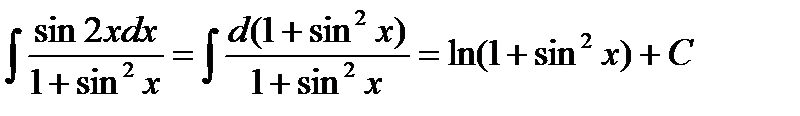 .
.
Пример 6.6.19. 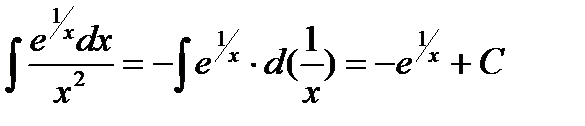 .
.
Пример 6.6.20. 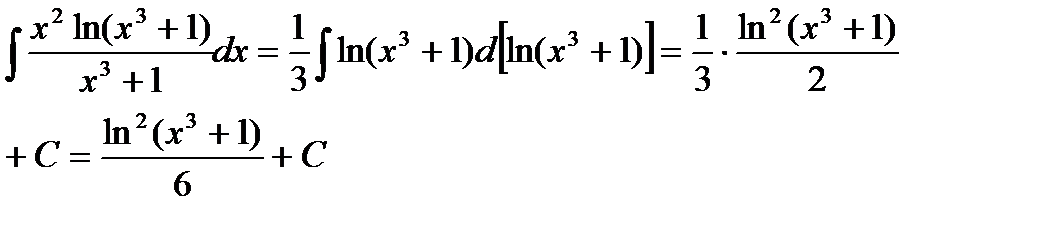 .
.
Заметив, что 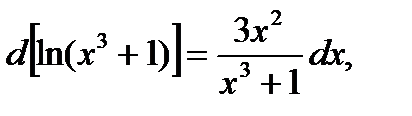 подведем под знак дифференциала
подведем под знак дифференциала 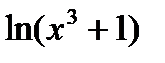
Дата добавления: 2016-06-05; просмотров: 2177;











