Кривые второго порядка

Канонические уравнения:

эллипса ,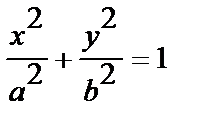

гиперболы ,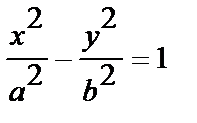

параболы ;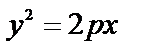

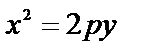
Эксцентриситеты

эллипса ,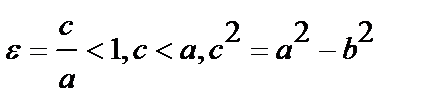

гиперболы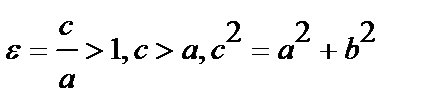

параболы ,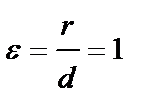

где rи d- расстояния любой точки параболы до фокуса и директрисы соответственно. Уравнение директрисы параболы ; .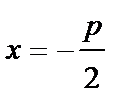

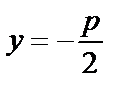Построение кривойв полярной системе координат

Полярная система координат задается точкойО(полюсом), выходящим из нее лучом и единицей масштаба. Полярные координаты точки М - два числа ρ и φ, первое из которых ρ (полярный радиус) равно расстоянию точки М от полюсаО, а второе φ (полярный угол) - угол, на который нужно повернуть полярный луч против часовой стрелки до совмещения с лучом ОМ.

Номер точки
j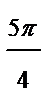
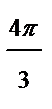
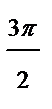
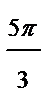
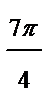
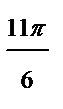
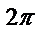
r	-0,1	0,5		-3,5	4,1	4,6

Обычно считают, что ρ и φ изменяются в пределах

,

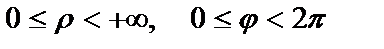чтобы соответствие между точками плоскости и полярными координатами было однозначным.

Замечание. В задачах, связанных с перемещением точки по плоскости (в механике), удобнее отказаться от этих ограничений, когда естественно считать, что при вращении точки угол может быть и больше 2π, а при движении точки по прямой, проходящей через полюс, считать, что при переходе через полюс полярный радиус точки меняет знак на отрицательный.

Пример 6.2.7. Построить график функции ρ = 2 + 3cos φ.

Построение выполняем поточечное. Выяснив область определения функции( 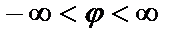), задаемся для начала значениями φ в интервале [0,2π] и вычисляем соответствующие значения ρ:

Номер точки
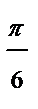
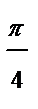
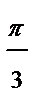
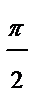
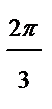
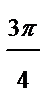
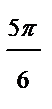
j									π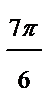
r		4,6	4,1	3,5		0,5	-0,1	-0,5	-1	-0,5

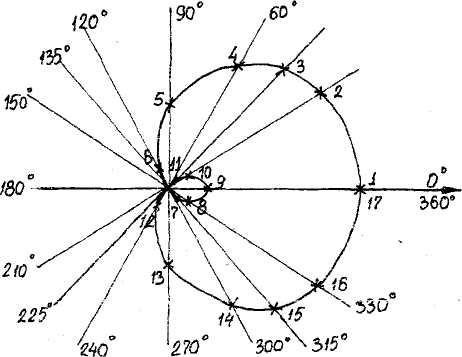Выполним построение с помощью транспортира.

Улитка Паскаля

При значениях 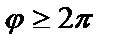полученные точки повторяются.

Замечание 1. Если форма кривой неясна, берем промежуточные точки.

Замечание 2. Наиболее часто встречающиеся кривые и их название приведены в справочнике [3] .