Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса
Рассмотрим систему, составленную из трех линейных алгебраических уравнений с тремя неизвестными.
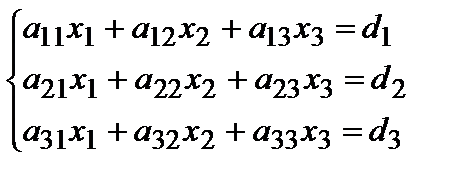 (6.1.11.)
(6.1.11.)
Решением (2.1)называется система 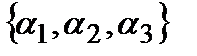 из трех чисел, удовлетворяющая требованию: если в (2.1) вместо
из трех чисел, удовлетворяющая требованию: если в (2.1) вместо 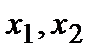 и
и 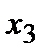 подставить соответственно
подставить соответственно 
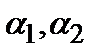 и
и 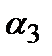 , то получим три верных равенства (три тождества).
, то получим три верных равенства (три тождества).
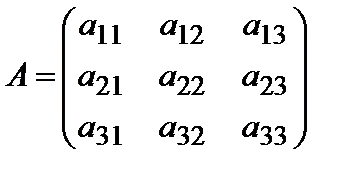 (6.1.12)
(6.1.12)
- основная матрица системы (2.1)
 (6.1.13)
(6.1.13)
- расширенная матрица (2.1)
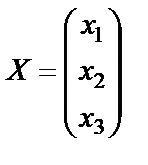 ;
; 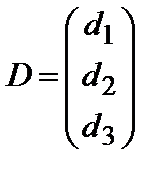 ;
; 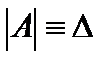 (6.1.14)
(6.1.14)
система (2.1) может быть записана в матричном виде так:
AX=D (6.1.15)
X – неизвестная матрица-столбец. Введем вспомогательные определители:
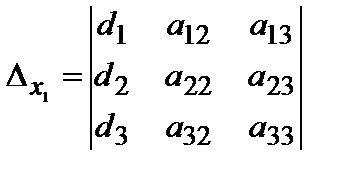
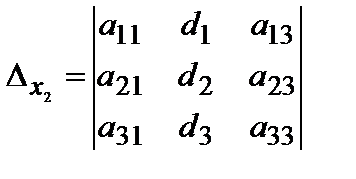
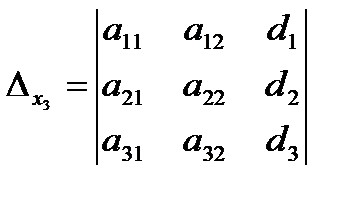
Предполагая, что матрица A - невырожденная и умножая (2.5) слева и почленно на A-1, получим
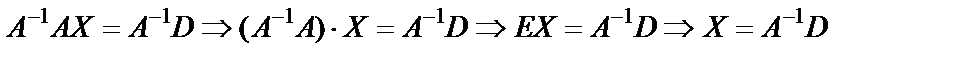 –(6.1.16) матричный способ решения системы.
–(6.1.16) матричный способ решения системы.
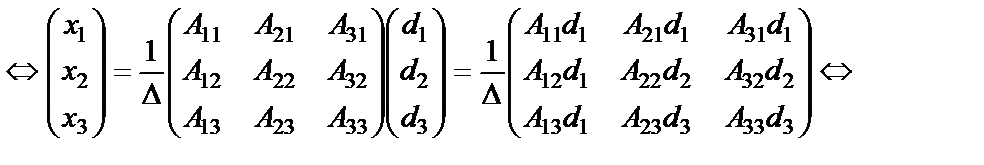
Используя понятие равенства двух матриц, получим
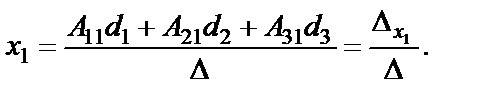 (6.1.17)
(6.1.17)
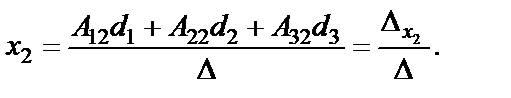 (6.1.18)
(6.1.18)
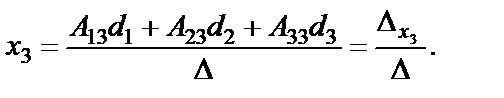 (6.1.19)
(6.1.19)
Элементарными преобразованиями матрицы называются следующие преобразования:
- Перестановка местами произвольных двух строк (столбцов).
- Умножение строки (столбца) на отличное от нуля число.
- Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число.
Пример 6. 1.2. Найти матрицу, обратную матрице 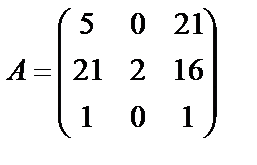 . Проверить результат.
. Проверить результат.
Обратную матрицу находим по формуле 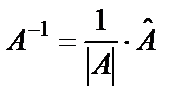 .
.
Вычислим определитель матрицы по правилу треугольника:
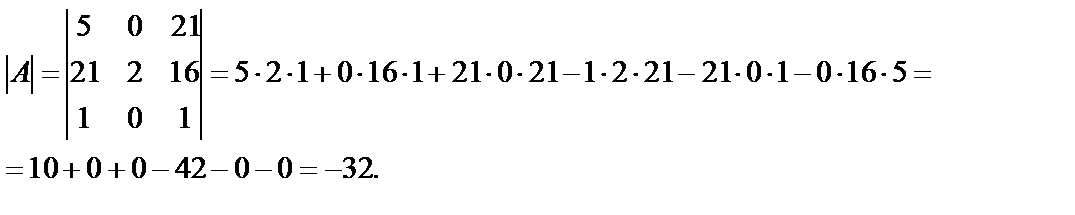
Определитель не равен нулю, следовательно, обратная матрица существует. Составляем матрицу из алгебраических дополнений ( 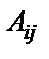 ) и транспонируем ее.
) и транспонируем ее.
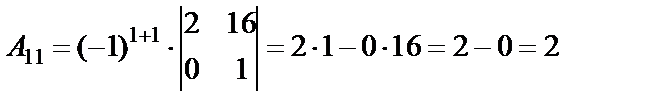 ;
;
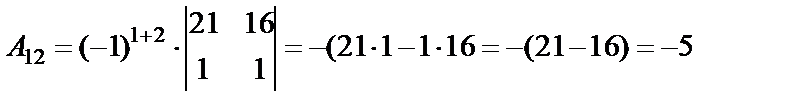 ;
;
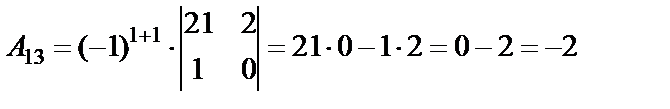 ;
;
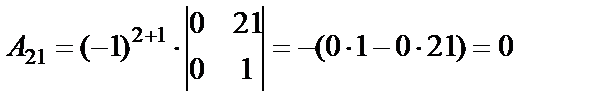 ;
;
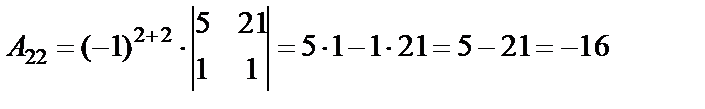 ;
;
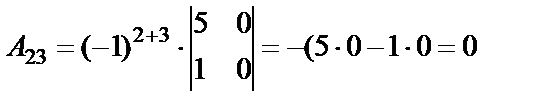 ;
;
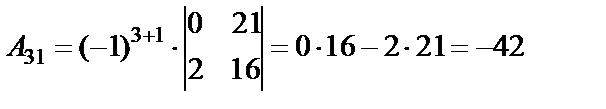 ;
;
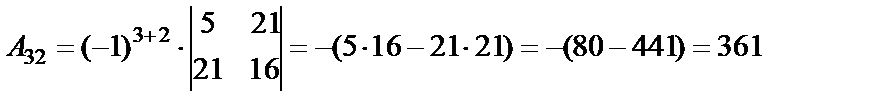 ;
;
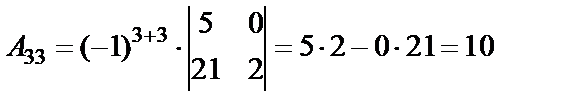 ;
;
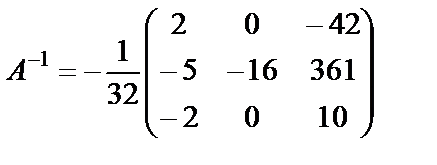 .
.
Выполним проверку:
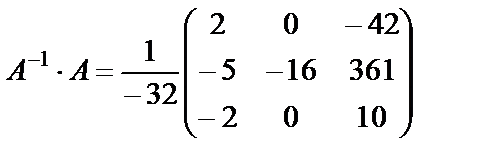 ·
· 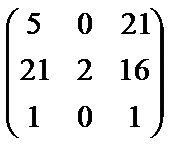 =
=
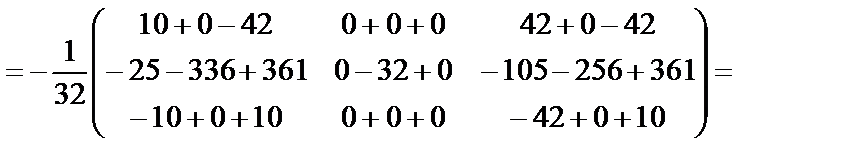
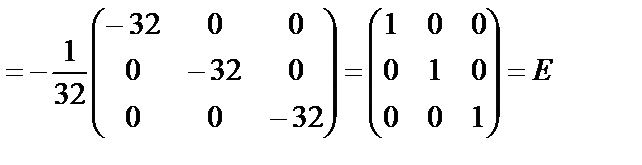 .
.
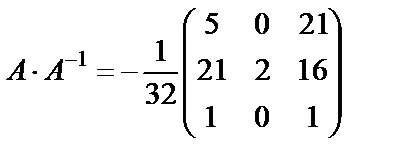 ·
· 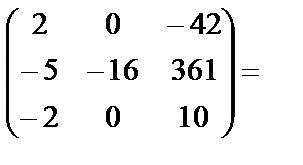
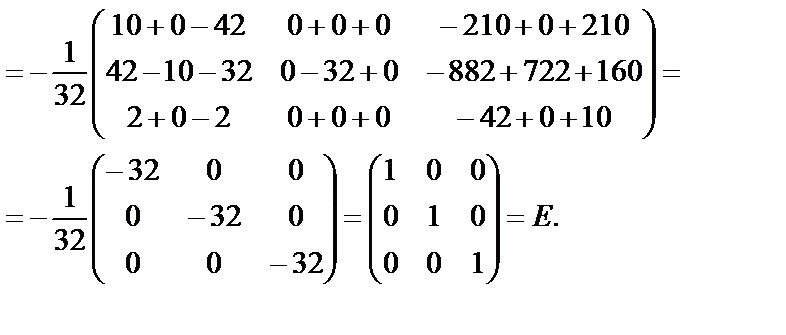
Получим: A-1×A=A×A-1=E. Следовательно, обратная матрица найдена верно.
Ответ: 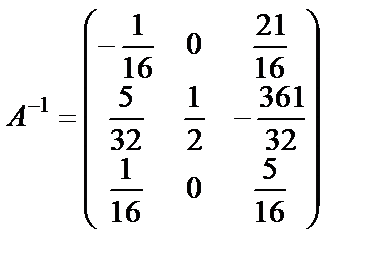 .
.
Пример 6.1.3. Решить систему линейных уравнений по формулам Крамера
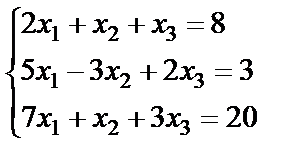 .
.
Решение:
Найдем главный определитель системы
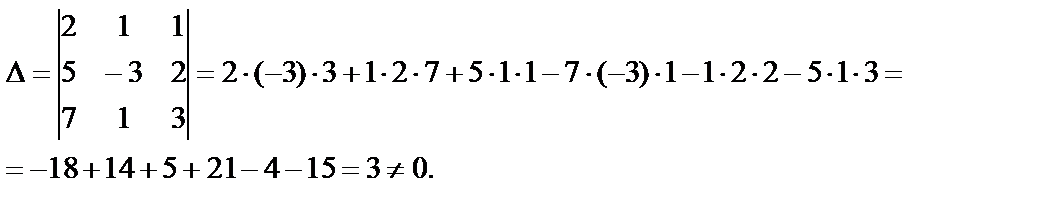
Так как число уравнений и число неизвестных системы между собой равны m=n=3 и определитель отличен от нуля, система имеет единственное решение.
Найдем вспомогательные определители:
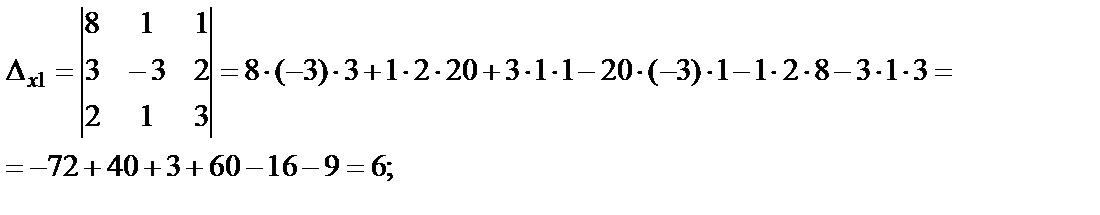
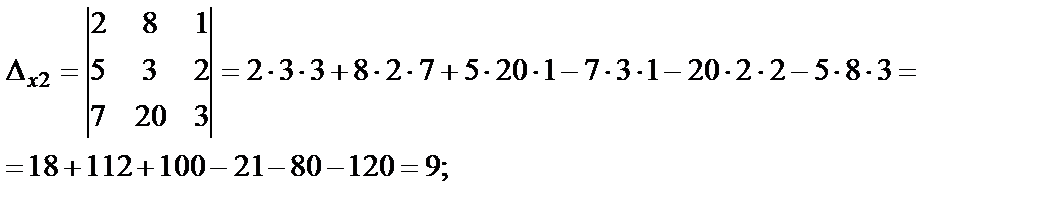
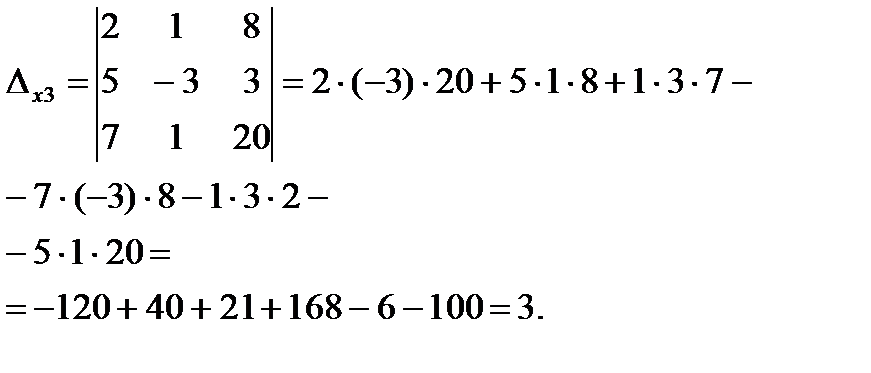
Неизвестные находим по формулам Крамера:
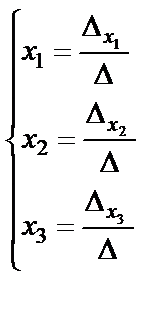 ;
; 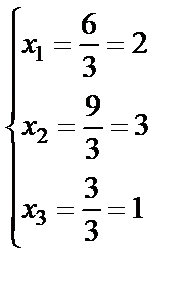 .
.
Ответ: 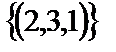 .
.
Пример 6.1.4.. Решить систему линейных уравнений методом Гаусса
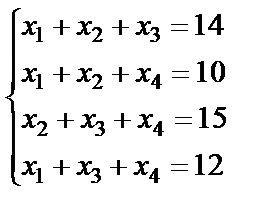 .
.
Решение.
Метод Гаусса – это метод последовательного исключения неизвестных преобразованием данной системы линейных уравнений к эквивалентной. Преобразования уравнений системы заменяются преобразованием строк расширенной матрицы системы до приведения основной матрицы к треугольной или трапециевидной форме. Обнуление элементов выполняется элементарными преобразованиями матрицы(умножение строк на числа, отличные от нуля с последующим сложением).
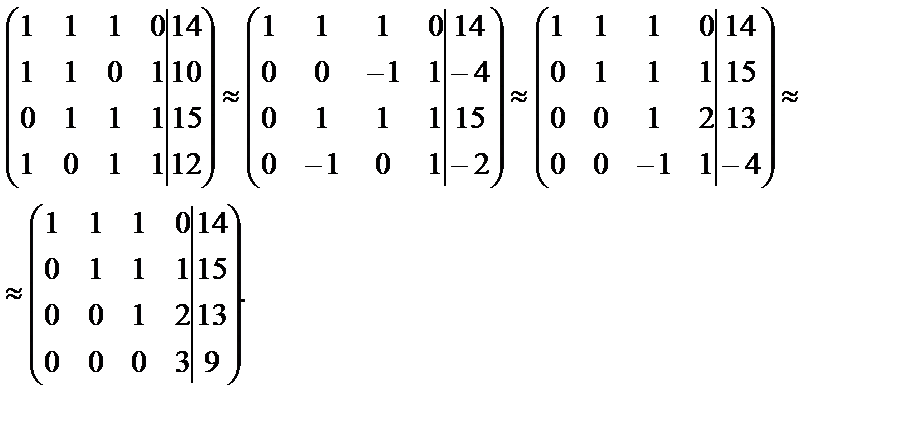
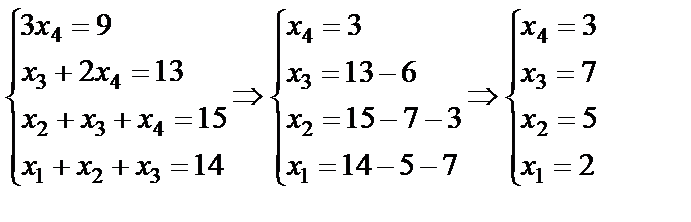 .
.
Ответ: 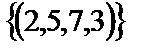 .
.
Пример 6.1.5. Применить теорему Кронекера – Капели и найти все решения системы методом Гаусса 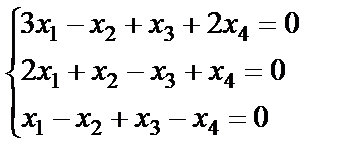 .
.
Решение.
Однородная матрица всегда имеет тривиальное решение, в данном случае (0;0;0;0), поэтому нас интересуют другие решения системы.
Применяем метод Гаусса:
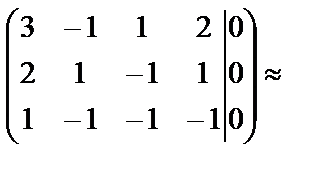
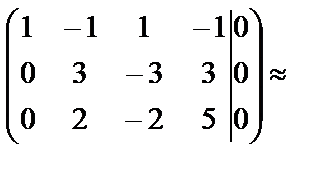
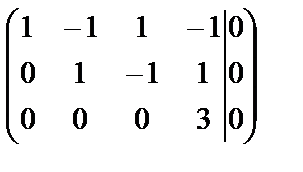 .
.
Так как размерности основной и расширенной матриц системы 3x4 и 3x5 соответственно, ранги этих матриц не могут превышать числа 3. Попробуем посмотреть, есть ли для этих матриц минор третьего порядка, отличный от нуля. Составим его из первых двух и четвертого столбца: 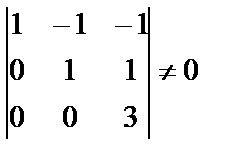 , так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Следовательно, ранги основной и расширенной матриц равны 3. По теореме Кронекера-Капелли данная система совместна. Так как число уравнений m=3 меньше числа неизвестных n=4, то она имеет бесчисленное множество решений. Закрепленных (базисных) переменных будет 3 (так как r=3), свободных переменных будет (n-r=4-3=1) одна. Минор, который мы составили выше, называется базисным, а переменные, входящие в него, базисными. Следовательно,
, так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Следовательно, ранги основной и расширенной матриц равны 3. По теореме Кронекера-Капелли данная система совместна. Так как число уравнений m=3 меньше числа неизвестных n=4, то она имеет бесчисленное множество решений. Закрепленных (базисных) переменных будет 3 (так как r=3), свободных переменных будет (n-r=4-3=1) одна. Минор, который мы составили выше, называется базисным, а переменные, входящие в него, базисными. Следовательно, 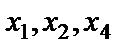 - базисные переменные, а
- базисные переменные, а 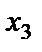 - свободная, то есть
- свободная, то есть 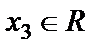 . Выполним обратный ход метода Гаусса:
. Выполним обратный ход метода Гаусса:
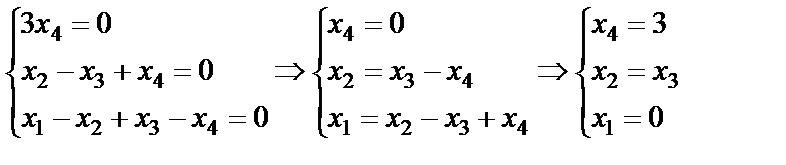 .
.
Решением системы будет множество четверок чисел 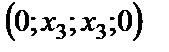 , где
, где 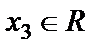 .
.
Например, (0;2;2;0), (0;-1;-1;0), 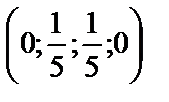 - решения системы.
- решения системы.
Ответ: 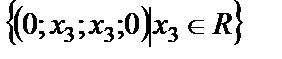 .
.
Замечание. Обратите внимание, что тривиальное решение тоже задается этим множеством.
Пример 6. 1.6. Даны координаты векторов 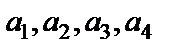 и
и 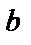 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 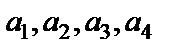 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 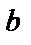 в этом базисе.
в этом базисе.
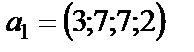 ;
; 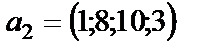 ;
; 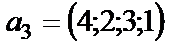 ;
; 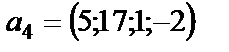 ;
; 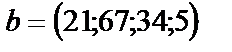 .
.
Решение.
Если векторы 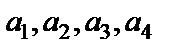 образуют базис, то существует разложение вектора
образуют базис, то существует разложение вектора 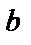 в этом базисе
в этом базисе 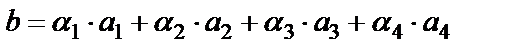 , то есть
, то есть
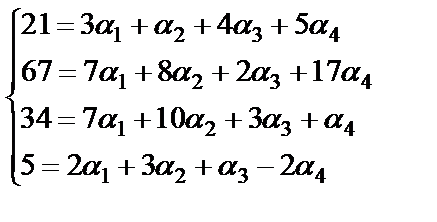 .
.
Отсюда вытекает решение задачи: найти координаты вектора 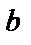 в базисе
в базисе 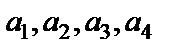 означает решить систему четырех уравнений с четырьмя неизвестными
означает решить систему четырех уравнений с четырьмя неизвестными 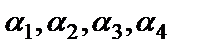 . Эта система будет иметь единственное решение, если ее основной определитель будет отличен от нуля.
. Эта система будет иметь единственное решение, если ее основной определитель будет отличен от нуля.
Решаем методом Гаусса:

Так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали , видим, что он отличен от нуля. Следовательно, векторы 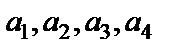 независимы и образуют базис.
независимы и образуют базис.
Найдем координаты вектора b в этом базисе
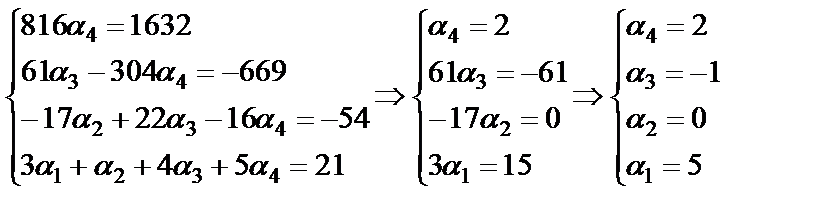 .
.
Следовательно, 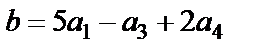 или b=(5;0;-1;2) в базисе
или b=(5;0;-1;2) в базисе 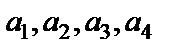 .
.
Ответ: 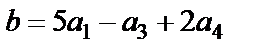 .
.
Дата добавления: 2016-06-05; просмотров: 3901;











