Линейная система сравнения.

Заменим нелинейный блок N пропорциональным звеном с коэффициентом усиления μ. В этом случае схема на рисунке 1 преобразуется в линейную систему, которую будем называть линейной системой сравнения (ЛСС). Из определения абсолютной устойчивости следует, что полученная линейная система должна быть устойчива для всех значений коэффициента усиления μ, заданных неравенством

μ₁ < μ < μ₂ (6)

в частности, если μ₁ = 0, то неравенство (6) принимает вид

0 < μ < μ₀ (7)

Для обозначения секторов (отрезков) устойчивости ЛСС будем использовать вместо буквы S букву L.

Первым этапом при решении задачи об абсолютной устойчивости исходной системы в заданном классе S(μ₀) или S(μ₁, μ₂) является исследование устойчивости линейной системы сравнения при изменении коэффициента усиления μ в соответствии с (6). Если хотя бы для одного значения μ из (6) линейная система сравнения окажется неустойчивой, то исходная система заведомо не является абсолютно устойчивой.Более того, в лучшем случае мы получим автоколебания, а в худшем – расходящийся процесс.

Обозначим передаточную функцию блока L ЛСС

W(p) = B(p)/A(p) (8)

Обратим внимание, что коэффициент усиления «включён» в многочлен B(p), т.е. коэффициенты многочлена B(p) умножены на величину коэффициента усиления. Передаточная функция разомкнутой линейной системы сравнения равна

μ ·W(p), (9)

а характеристическое уравнение ЛСС имеет вид

A(p) + μB(p) = 0 (10)

Для изучения устойчивости ЛСС будем использовать, в силу традиций, критерий Найквиста в нормированной форме (точка -1 заменяется точкой -μ^-1) , хотя применение корневого годографа было бы более наглядно.

Устойчивость и предельная устойчивость ЛСС для базового случая S(μ₀)

Рассмотрим вопрос об устойчивости ЛСС в зависимости от расположения полюсов W(p).

1. предположим, что W(p) имеет хотя бы один неустойчивый полюс, в этом случае ЛСС будет неустойчива при малых значениях коэффициента усиления μ и, следовательно, положение равновесия исходной нелинейной системы заведомо будет неустойчиво.

2. предположим, что W(p) имеет только устойчивые полюса (состоит из устойчивых звеньев). В этом случае величина μ₀ должна удовлетворять условию, что левее точки –μ₀^-1 кривая Найквиста не пересекает отрицательную часть действительной оси. (в противном случае нарушается устойчивость ЛСС при некоторых значениях μ меньших, чем μ₀).

Указанные ограничения существенны при исследовании, так называемых, условно устойчивых (по Боде) линейных систем. Эти системы имеют несколько секторов устойчивости совершенно равносильных с точки зрения линейной теории.Но в нелинейных задачах положение радикально меняется. Равносильность исчезает. Только крайний левый бесконечный сектор определяет число μ₀. для примера на рисунке 8 приведена кривая Найквиста условно устойчивой системы. Предполагается, что все полюса W(p) находятся в левой полуплоскости.

Обратимся к рисунку 8.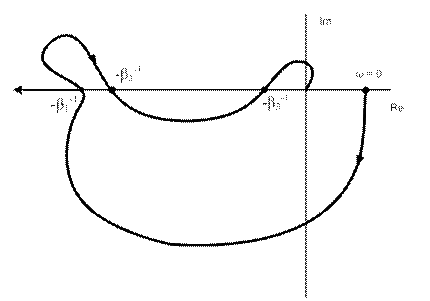

Рис. 8

ЛСС устойчива при следующих значениях коэффициента усиления μ:

L(0, β₁): 0 < μ < β₁ (11)

L(β₂, β₃): β₂ < μ < β₃ (12)

В данном случае наибольшее значение μ₀ можно взять равное β₁ .

3. Предположим, что W(p) имеет полюса в левой полуплоскости и на мнимой оси и рассмотрим вопрос, когда при малых значениях коэффициента усиления μ полюса сдвигаются с мнимой оси в левую полуплоскость. Это условие в теории абсолютной устойчивости называется «предельной устойчивостью». Для выполнения условия предельной устойчивости требуется, чтобы дуги окружности бесконечного радиуса, порожденных полюсами W(p) на мнимой оси, не пересекали отрицательную часть действительной оси.

Практический интерес представляют следующие случаи:

1. одно интегрирующее звено, остальные звенья устойчивые;

2. два интегрирующих звена, остальные звенья устойчивые;

3. одно консервативное звено, остальные звенья устойчивые;

4. одно консервативное и одно интегрирующее звено.

В первом случае условие заведомо выполняется.

Для изучения вопроса о том, как расположены дуги окружности бесконечного радиуса, разлагаем передаточные функции на простые дроби (это удобно делать с помощью Mathсad)

Два интегрирующих звена:

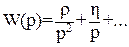(13)

В этой формуле и ниже отточием указаны слагаемые имеющие полюса в левой полуплоскости.

В окрестности точки ω=0 можно принять

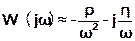(14)

Если выполняются неравенства ρ>0 и η>0 , то дуга окружности бесконечного радиуса не пересекает отрицательной части действительной оси, как показано на рисунке 9.

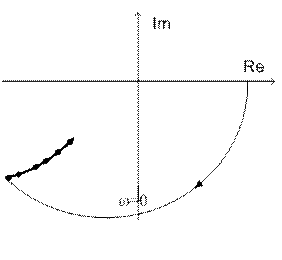
Рис. 9

Консервативное звено. Пусть его полюсы на мнимой оси - ±jΩ. Разлагаем на простые дроби:

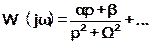(15)

В окрестности точки ω = +Ω можно принять:

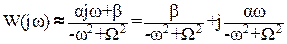(16)

Если α>0, то дуга окружности бесконечного радиуса не пересекает отрицательную часть действительной оси. В зависимости от знака числа β возможны два варианта, показанные на рисунке 10.

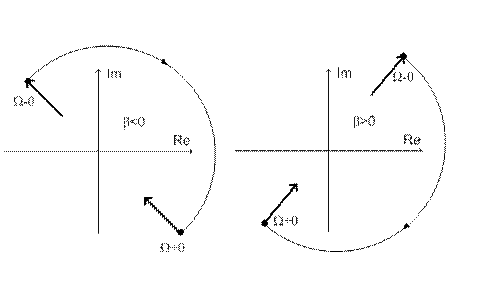
рис.10

Консервативное и интегрирующее звенья:

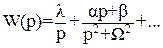(17)

В данном случае необходимо учитывать две дуги окружности бесконечного радиуса. Если α>0 и λ>0, то обе дуги не пересекут отрицательной части действительной оси (см. рис. 11).

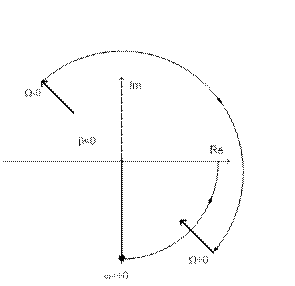
Рис.11

Таким образом, указанны условия, при которых ЛСС будет устойчива при малых коэффициентах усиления μ.

Упражнение. Доказать, что если W(p) содержит три интегрирующих звена, то ЛСС заведомо не будет устойчива при малых коэффициентах усиления.

Перейдём к рассмотрению общего случая S(μ₁, μ₂).

Вне зависимости от того устойчива или нет передаточная функция W(p), необходимо, чтобы ЛСС была устойчива для всех значений μ, удовлетворяющих неравенству:

μ₁ < μ < μ₂ (18)

Отметим, что W(p) может иметь неустойчивые звенья, например:

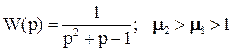
Характеристическое уравнение ЛСС: 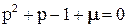устойчиво.

Ниже приводятся некоторые рисунки, для определения устойчивости ЛСС по критерию Найквиста.

Критерий Найквиста для всех μ, удовлетворяющих условию 0 < μ < μ₀

W(p) = 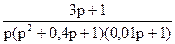  Рис. 12а.	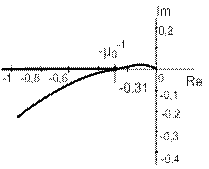Рис. 12b.
W(p) = 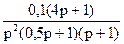Рис. 13a.	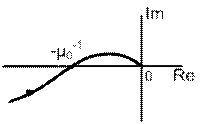Рис. 13b.
W(p) = 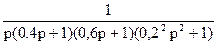Рис. 14.

Критерий В.М. Попова. Достаточное условие абсолютной устойчивости положения равновесия нелинейной системы в классе S(μ₀).

Сначала отметим одну терминологическую особенность. Обычно в математике термин «критерий» употребляется в случае необходимых и достаточных условий (например, критерий Гурвица, критерий Найквиста). Однако, в теории абсолютной устойчивости термин «критерий» употребляют в случае, когда известны только достаточные условия.

При изучении критерия В.М.Попова по умолчанию будем предполагать, что проведено исследование ЛСС и установлена её устойчивость и предельная устойчивость, если W(p) имеет полюса на мнимой оси.

Начнем рассмотрение с описания неравенства В.М. Попова, которое имеет исключительно важное значение для нашей задачи.

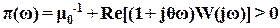(19)

Неравенство (19) условимся называть неравенством В.М.Попова.

На первый взгляд, кажется, что проверить выполнение неравенства В.М.Попова для заданного числа μ₀ и передаточной функции W(p) очень трудно, т.к. ничего не известно о числе θ. Однако, существует исключительно простой геометрический метод его проверки, который будет описан ниже.

Основная теорема.

1. Пусть W(p) имеет все полюса в левой полуплоскости кроме, быть может, простого полюса в нуле (иначе: пусть W(p) содержит только устойчивые звенья и, быть может, одно интегрирующее звено). В этом случае для абсолютной устойчивости положения равновесия нелинейной системы в классе S(μ₀) достаточно выполнение неравенства В.М.Попова.

2. Если W(p) не содержит интегрирующего звена, а содержит только устойчивые звенья, то выполнение неравенства В.М.Попова достаточно для абсолютной устойчивости положения равновесия в классе S[μ₀].

3. Пусть W(p) содержит устойчивые звенья и два интегрирующих звена. Для того чтобы положение равновесия было абсолютно устойчивым в классе S(μ₀) достаточно выполнение неравенства В.М.Попова и расходимости двух приведённых ниже интегралов

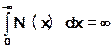
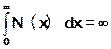(20)

Важно подчеркнуть, что фактически нет необходимости в вычислении интегралов. Их расходимость будет обеспечена, если график N(x) находится на конечном расстоянии от оси абсцисс. В этом случае величина μ₀ не имеет значения, как будет видно из дальнейшего, для выполнения неравенства В.М.Попова.

4. Пусть W(p) наряду с устойчивыми звеньями содержит одно консервативное звено с полюсами ±jΩ и , быть может, одно интегрирующее звено. В этом случае для абсолютной устойчивости положения равновесия в классе S(μ₀) достаточно выполнение неравенства В.М.Попова для всех ω≠Ω. Причём число θ определяется однозначно: 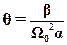(21)

где α и β коэффициенты в разложении W(p) на простые дроби.

В 1961 году была напечатана работа молодого румынского математика В.М.Попова «об абсолютной устойчивости нелинейных систем автоматического регулирования» в журнале «Автоматика и телемеханика» №8. это выдающаяся и исключительно оригинальная работа послужила поворотным пунктом в истории развития теории устойчивости. В дальнейшем значительный вклад в развитие теории абсолютной устойчивости внесли советские математики. Особенно В.А.Якубович.

Условие 3 и 4 данной теоремы были доказаны советским учёным В.Е.Якубовичем (ЛГУ) в 1964 году.