Частотные критерии абсолютной устойчивости положения равновесия и отрезка покоя.

Постановка задачи.

Рассмотрим вопрос об устойчивости единственного положения равновесия нелинейной системы, структурная схема которой приведена к каноническому виду (рис. 1), где обозначено: линейный блок L и нелинейный блок N.

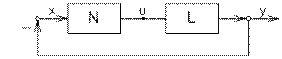
Рис. 1

Линейный блок L задан передаточной функцией W(p). Будем предполагать, что W(p) – правильная рациональная дробь. Никаких ограничений на степень знаменателя W(p) не налагается. Рассматриваются системы произвольно высокого порядка. Должны быть известны, если они есть, корни знаменателя на мнимой оси и в правой полуплоскости.

Нелинейный блок N.Функция u = N(x), связывающая сигналы на входе и на выходе блока, известна не полностью. Задается только класс функций, которому принадлежит N(x), а не её график или аналитическое выражение. Этот класс определяется следующими условиями:

1. График функции N(x) находится внутри двухполосного сектора, ограниченного прямыми (1) (рис. 2, 3)

u = μ₁x и u = μ₂x (1)

Если граничные прямые включаются в сектор, то условимся сектор обозначать S[μ₁, μ₂] или S[μ₀]. Если не включаются, то – S(μ₁, μ₂₎ или S(μ₀).

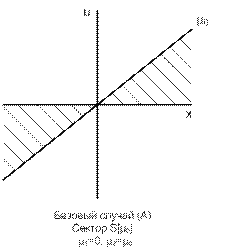Рис. 2

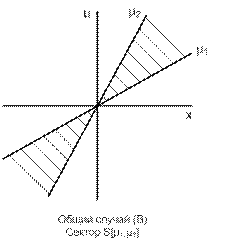Рис. 3

2. Функция N(x) является однозначной, кусочно-непрерывной и может, вообще говоря, иметь конечные разрывы первого рода. Функция N(x) обращается в нуль только при значении x равном нулю.

Вначале мы не будем рассматривать случай, когда имеет место отрезок покоя. Далее будет кратко рассмотрен вопрос об устойчивости отрезка покоя системы (т.е. система, у которой нелинейный элемент имеет зону нечувствительности) и случая, когда N(x) есть функция с гистерезисом.

Условие, что функция N(x) находится в секторе S[μ₁, μ₂] можно записать в форме неравенства

μ₁ ≤ N(x)/x ≤ μ₂ , x ≠ 0 (2)

случай, когда μ₁ = 0 называется базовым:

0 ≤ N(x)/x ≤ μ_{0 ,} x ≠ 0 (3)

Для упрощения рассуждений целесообразно отказаться от условия, что N(x) может касаться ограничивающий сектор прямых и в формулах (2) и (3) перейти к строгим неравенствам, которые соответственно будем обозначать круглыми скобками.

μ₁ < N(x)/x < μ₂ , x ≠ 0 (4)

0 < N(x)/x < μ₀ , x ≠ 0 (5)