Геометрический метод решения неравенства В.М.Попова.

Разделим W(jω) на действительную и мнимую часть.

W(jω) = U(ω) + jV(ω) (22)

Выполним следующие преобразования:

Re[(1 + jωθ)W(jω)] = Re[(1 + jωθ)[U(ω) + jV(ω)]] =

(23)

= Re[U(ω) + jωθU(ω) + jV(ω) – θωV(ω)] = U(ω) – θωV(ω)

Неравенство В.М.Попова можно согласно (23) записать :
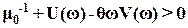(24)

Обозначим:

X = U(ω) , Y = ωV(ω) (25)

Для сокращения при записи функций X и Y опущена зависимость от переменной ω.

Неравенство (24), используя обозначения (25), запишем в следующей форме:

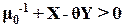(26)

Введём в рассмотрение плоскость с координатами XY. Проведём на этой плоскости прямую, которую назовём прямой В.М.Попова:

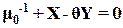(27)

Прямая (27) пересекает ось абсцисс в точке 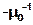и имеет наклон .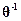

Прямая В.М.Попова разбивает плоскость на две полуплоскости. Для точек одной из них выполняется неравенство (26). Очевидно, что это будет полуплоскость, в которой расположена точка X=0, Y=0.

Построим на плоскости XY параметрическую кривую, определяемую соотношением (25), изменяя переменную ω от нуля до бесконечности. Обозначим построенную кривую T(ω). Перейдём к построению прямой В.М.Попова. Так как нет ограничений на величину θ, то эту прямую можно провести через точку x= 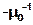под любым наклоном. Возможны два варианта.

Первый. Через точку 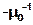возможно провести прямую В.М.Попова таким образом, чтобы кривая T(ω) была расположена целиком справа от этой прямой (так как на прямой не указывается направление ориентации, то уточним, что выражением «справа от прямой» подразумевают полуплоскость, содержащую начало координат)

Второй. Через точку 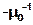невозможно провести прямую В.М.Попова. Любая прямая, проведённая через точку x= 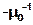пересекает кривую T(ω), или кривая T(ω) находится слева от прямой.

Если имеет место первый вариант, значит для всех точек кривой T(ω) выполняется неравенство В.М.Попова для значения параметра θ, определяемого наклоном прямой.

Если имеет место второй вариант, то неравенство В.М.Попова не может быть удовлетворено при любом значении параметра θ.

Из приведённых рассуждений следует вывод.

Чтобы проверить выполняется или нет неравенство В.М.Попова для данной частотной передаточной функции W(j ω) надо построить график T(ω) по соотношению (25), затем проверить возможно или нет провести через точку 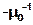прямую В.М.Попова таким образом, чтобы T(ω) была расположена справа от этой прямой.