Рассмотрим вычисление параметров автоколебаний с помощью точечного преобразования.

Очевидно, что все фазовые траектории системы пересекают прямую

x + y = 1

поэтому можно рассмотреть точечное преобразование этой прямой «в себя». Однако, задача может быть упрощена за счет симметрии системы.

запишем уравнения границ листов:

x + y = 1 (13)

x + y = -1 (14)

Пусть начальная точка принадлежит уравнению (9), а конечная точка - уравнению (10). Начальную точку обозначим (x,y), конечную – (x₁,y₁). Траектория движения имеет вид:

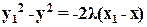(15)

Исключая значения x и x₁ из уравнения соответственно (13) и (14), получаем:

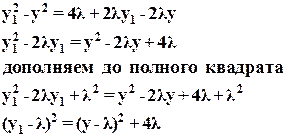(16)

Извлекаем корень и получаем соотношение:

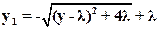(17)

В качестве последующей точки точечного преобразования берём

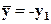(18)

И получаем формулу точечного преобразования:

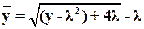(19)

Неподвижная точка этого точечного преобразования

y* = 1

эта неподвижная точка соответствует симметричному предельному циклу, показанному на рисунке 7.

Для диаграммы Кенигса-Ламерея для случая λ>1 и λ<1 приведены на рисунках 8 и 9.

Диаграмма Кенигса-Ламерея.

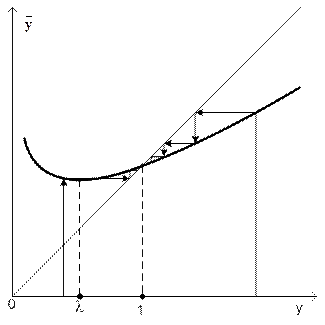
Рис. 8

1-й вариант

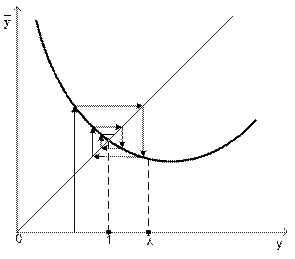
Рис. 9

2-й вариант

· Пример системы с ограниченным непериодическим движением устойчивым по Пуассону.

В заключение исследования динамики релейных систем с двумя интеграторами приведем, по-видимому, простейший пример системы с непериодическим движением, описанный Э.В.Гаушусом .

Предположим, что передаточная функция имеет вид:

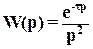(20)

Нелинейный элемент представляет собой трёхпозиционное реле с опережением, показанное на рисунке 10. Напомним свойства трёхпозиционного реле с опережением. Переключение реле в точках x = b и x = a зависит от знака производной функции x(t) и состояния реле. Если в точке «b» производная отрицательна (x’<0) и N(x+0) = 1, то переключение происходит с +1 на 0, как показано на рисунке стрелкой. Если же в точке «b» производная положительна (x’>0) и N(x-0) = 0, то реле переключается со значения 0 на значение +1, как показано пунктиром. В точке «a», если x’>0 и N(x-0) = 0, то происходит переключение реле с 0 на +1, как показано на рисунке стрелкой. Но если x’<0 и N(x+0) = 1, то реле переключается со знака +1 на 0, как показано пунктиром.

Разбиение фазовой плоскости на листы без учёта запаздывания показано на рисунке 11.

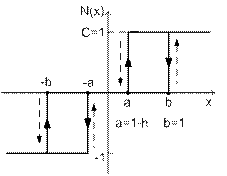Рис.10

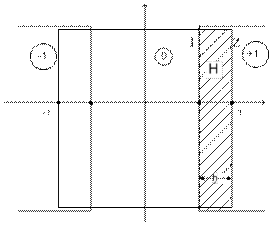Рис.11 Трёхлистная фазовая плоскость.

Из соображения симметрии можно ограничиться рассмотрением только одной правой полуплоскости. На рисунке 11 граница нулевого листа обозначена буквой «Z», а граница листа +1 – «I». Полоса, где листы накладываются, обозначена буквой «Н».

Сначала предположим, что запаздывание равно нулю.

Фазовый портрет системы в этом случае будет иметь вид, показанный на рисунке 12.

Рассмотрим движение в первом квадранте. Изображающая точка переходит с листа «0» на лист «1» по границе листа «1» – линии «I». На листе «0» изображающая точка движется по горизонтальной прямой, а на листе «+1» она будет двигаться по параболе. Если переход с нулевого листа происходит ниже точки α, например в точке β, то парабола целиком располагается в полосе «Н» и в четвёртом квадранте перейдёт с листа «+1» на лист «0» по линии «I» в точке –β. В том случае, когда переход с листа «0» на лист «+1» происходит выше точки α, например в точке δ, то ситуация радикально меняется. Парабола выходит за линию «Z» и в четвертом квадранте переход с листа «+1» на лист «0» произойдет не по линии «I», а по линии «Z» в точке ξ, как показано на рисунке 12.

Фазовый портрет характеризуется тем, что при больших отклонениях изображающей точки имеет место процесс демпфирования, т.к. она стремится в замкнутую область с центром в начале координат – область консервативных движений.

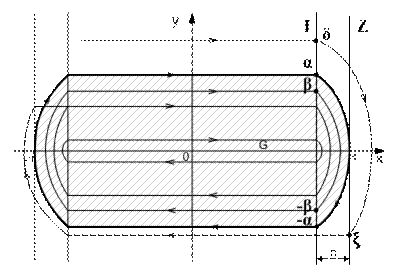Рис. 12

Подчеркнем, что на рисунке 12 нет предельных циклов. Заштрихованная область состоит из вложенных друг в друга замкнутых кривых.

Теперь перейдем к рассмотрению более сложного случая, когда имеет место запаздывание.

Запаздывание деформирует границы листов, как показано на рисунке 13.

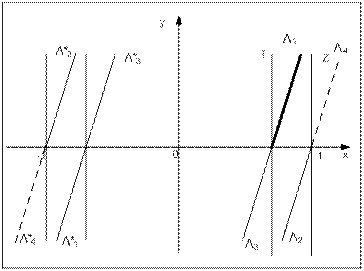
Рис. 13

Границы листов – вертикальные прямые «I» и «Z» наклоняются вправо. Область «Н» заключена между Λ₁ Λ₃ и Λ₂ Λ₄. Отметим, что буквой Λ с индексом на рисунке 13 и ниже обозначаются не точки, а полупрямые, исходящие из точек x = 1 – h и х = 1.

Ясно, что все траектории будут пересекать полупрямую Λ₁, поэтому ее можно принять за отрезок Γ и рассмотреть точечное преобразование полупрямой Λ₁ в себе. Однако, из соображений симметрии можно ограничиться рассмотрением точечного отображения полупрямой Λ₁ в полупрямую Λ₁*.

На основании уравнения траекторий можно получить уравнения полупрямых Λ₁ Λ₂ Λ₃.

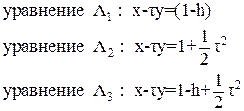(21)

Точки отрезков однозначно определяются их ординатой y, поэтому будем рассматривать функцию последования:

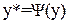. (22)

Покажем, что точечное преобразование Ψ в данном случае будет разрывной функцией. Для этого обратимся к рисунку 14. Из этого рисунка видно, что точечное преобразование имеет разрыв в точке y = α. Значение α определяется тем условием, что изображающая точка, перейдя с листа «0» на лист «+1», будет двигаться по параболе, проходящей через точку х = 1, то есть она выйдет на границу полосы «Н». Если изображающая точка пересекает линию Λ₁ при значениях y меньших, чем α (в точке β₀), то парабола целиком пройдет внутри полосы «Н». Переход с листа «+1» на лист «0» произойдет на линии Λ₃ в точке ξ₁. В том случае, если изображающая точка пересечет линию Λ₁ при значениях y больших α (в точке β₂), то парабола выйдет за границу полосы «Н», пересечет ось абсцисс в точке δ₂ и перейдет с листа «+1» на лист «0» уже не на полупрямой Λ₃ а на полупрямой Λ₂ в точке ξ₂.

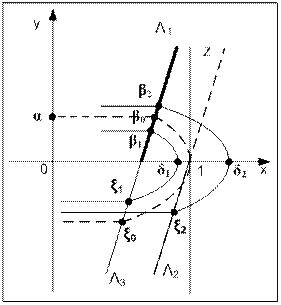
Рис. 14

Аналитическое выражения для функции последования будет иметь следующий вид:

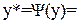
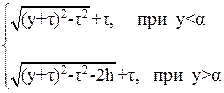(23)

В фазовом портрете на рисунке 15 изображающая точка, попадая в некоторую замкнутую область, не совершает там движения по замкнутой траектории, а начинает неограниченно «петлять», т.е. имеют место ограниченные непериодические движения.

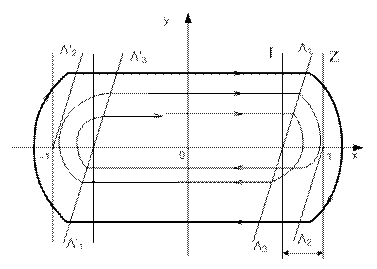Рис.15

Диаграмма Кенигса-Ламерея в данном случае будет иметь вид показанный на рисунке 16.

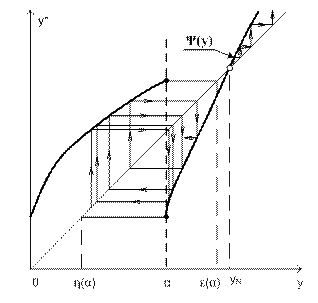
Рис. 16

На диаграмме Кенигса-Ламерея есть одна неподвижная точка, координата которой равна

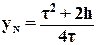(24)

Эта неподвижная точка неустойчива.

Из рисунка видно, что изображающая точка, попав в интервал η(α)<y<ε(α) уже никогда его не покинет.

Если изображающая точка находится в интервале: η < y < ε , то система совершает ограниченное непериодическое движение устойчивое по Пуассону (квазипериодические колебания).

Условие возможности возникновения квазипериодических колебаний может быть записано в виде

ε < y* (25)

Условие 24 через параметры h и τ выражается в виде:

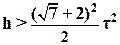(26)

или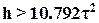

Таким образом, в системе существует квазипериодическое движение, ограниченное по координате y значениями η = τ и ε = .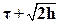

Для того, чтобы получить это движение, нам следует по заданной величине τ выбрать величину h и вычислить величину наибольшей величины начального условия y* по формуле 26. Если y > y*, то процесс заведомо расходится.

В заключение приведем пример процесса регулирования для τ=0,2;

h=0,5.

На рисунке 21 показаны графики выходного сигнала и сигнала на выходе релейного элемента для параметров:

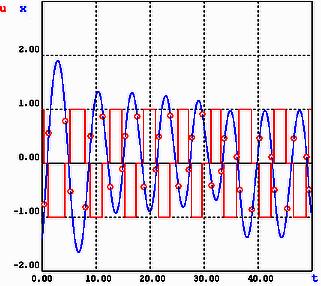
Рис. 21

Глава 12.