Форма фазовых траекторий релейных систем данного класса.

Определим форму фазовой траектории для системы данного класса. Покажем, что все фазовые траектории могут быть построены с помощью одного шаблона.

Запишем уравнение системы в простейшей форме, предварительно поменяв обозначение переменной с буквы z на букву х.

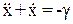(4)

От уравнения переходим к системе

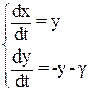(5)

По системе (5) записываем уравнение фазовых траекторий:

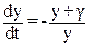(6)

Преобразуем:

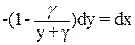(7)

Интегрируем:

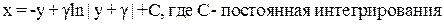(8)

Если γ=-1, то

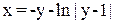(9)

Если y близок к единице, то

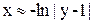(10)

Если γ=1, то

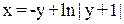(11)

Если y близок к минус единице, то

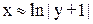(12)

Графики траекторий показаны на рисунке 3 и 4.

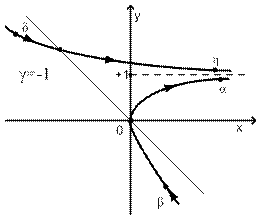Рис.3

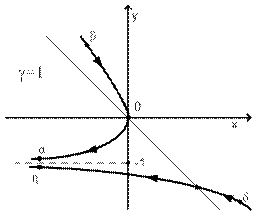Рис. 4

Траекторию на рисунке 4 можно получить с помощью траектории на рисунке 3. для этого следует перевернуть ее на 180º, закрепив в начале координат (иначе: заменить x, y на –х, -y и учесть, что |-y-1|=|y+1|).

Таким образом, вырезав шаблоны по траектории на рисунке 3, мы сможем с его помощью построить фазовый портрет для любой релейной системы с апериодическим и интегрирующим звеном.

Рассмотрим случай γ = 0.

Дифференциальное уравнение системы имеет вид в этом случае

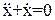(13)

Уравнению (13) соответствует система:

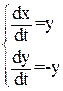(14)

Из системы (14) получаем уравнение фазовых траекторий:

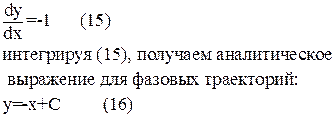
Таким образом, заключаем, что фазовые траектории системы на листе «0» будут отрезки прямых (16).

Запаздывание.

Влияние запаздывания на свойства системы скажется в том, что сигнал реле будет переключаться с опозданием на время τ. В течение промежутка времени τ изображающая точка будет двигаться по старой траектории, таким образом, запаздывание не изменит формы фазовых траекторий на листах, но деформирует вправо линии переключения изображающей точки с одного листа на другой, что, разумеется, может приводить к кардинально новым явлениям (по сравнению с тем случаем, когда запаздывание отсутствует), например, к возникновению автоколебаний.