Квадратный трехчлен


I. Функции

Общие свойства

В математическом анализе исходят из определения функции по Лобачевскому и Дирихле. Если каждому числу х из некоторого множества F чисел в силу какого-либо. закона приведено в соответствие число у, то этим определена функция от одного переменного х и в общем записывается y=f(x).».

Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у явля­ется функцией от переменной х. Значения зависи­мой переменной называют значениями функции. Символом f(x) обозначают значение функции, соответствую­щее значению аргумента, равному х.

Аналогично определяется функция, зависящая от нескольких переменных y=f(x)=f( ,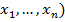

где х= (х 1, ..., х п) - точка n-мерного пространства; рассматривают также функции от точек

x=(x1, х2,...) некоторого бесконечномерного пространства, которые, впрочем, чаще называют функционалами.

Числовая функция определена на множестве D действительных чисел, если каждому значению переменной х поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Все значения независимой переменной образу­ют область определения функции. Все значения, которые принимает зависимая переменная, образу­ют область значений функции.
Если функция задана формулой и ее область оп­ределения не указана, то считают, что область оп­ределения функции состоит из всех значений аргу­мента, при которых формула имеет смысл.

Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы);
2. табличный способ (функция задается с помощью таблицы);
3. описательный способ (функция задается словесным описанием);
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскос­ти, абсциссы которых равны значениям аргу­мента, а ординаты — соответствующим значениям функции.
1 Нули функции
Нуль функции – такое значение аргумента, при котором значение функции равно нулю .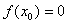
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
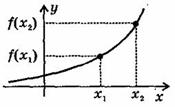
3 Возрастание (убывание) функции.

Возрастающаяв некотором промежутке функ­ция - функция, у которой большему значению аргу­мента из этого промежутка соответствует большее значение функции.

Функцияу = f (x)назы­вается возрастающейна ин­тервале (а; b), если для лю­бых x1 и x2 из этого интерва­ла таких, что x1< x2 , спра­ведливо неравенство f(x1)<f(x2).


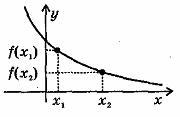
Убывающая в некотором промежутке функ­ция - функция, у которой большему значению аргу­ментаиз этого промежутка соответствует меньшее значение функции.
Функцияу =f (x)назы­вается убывающейна интер­вале (а; b), если для любых x1 и x2 из этого интервала таких, что x1< x2, справед­ливо неравенство f(x1)>f(x2).

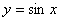
Ограниченная функция. Если существует такое число M, что 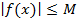. Например, функции

y=sinx иy=cosx, т.к. ,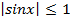


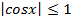
4. Четность (нечетность) функции
Четная функция - функция, у которой область определения симметрична относительно начала коор­динат и для любого х из области определения выпол­няется равенство f(-x) = f(x). График четной функ­ции симметричен относительно оси ординат.
Например, у = х2 - четная функция.
Нечетная функция - функция, у которой об­ласть определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечет­ной функции симметричен относительно начала координат.
Например: у = х3 - нечетная функция.
Функция общего вида не является четной или нечетной (у = х2+х).
Свойства некоторых функций и их графики


1.Линейной функциейГрафиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b) и параллельная прямой у = kx.
Прямая, не параллельная оси Оу, называется функция вида y=kx+b,где k и b – числа.
Область определения линейной функции – множество R действительных чисел.
является графиком линейной функции.

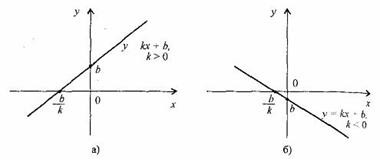
Свойства линейной функции.

1. При k > 0 функция у = kx + b возрастающая в области определения.
2. При k < 0 функция у = kx + b убывающая в области определения.
3. Множеством значений функции y = kx + b (k ≠ 0) является вся числовая прямая, т.е. множество R действительных чисел.
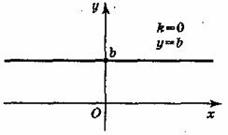
При k = 0 множество значений функции у = kx + b состоит из од­ного числа b.

 

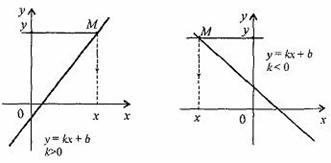
3. При b = 0 и k = 0 функция не является ни четной, ни нечетной.
При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она явля­ется четной.
При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.
Графиком линейной функции у = b является прямая, проходящая через точку (0; b) и параллельная оси ^ Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох.

5. При k > 0 имеем, что у > 0, если 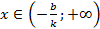и у < 0, если 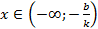. При k < 0 имеем, что у > 0, если 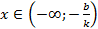и у < 0, если .

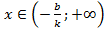2. Функция y = x2

Область определения этой функции - множество R действитель­ных чисел.
Придавая переменной х несколько значений из области опреде­ления функции и вычисляя соответствующие значения у по формуле y = x2 , изображаем график функции.

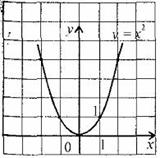
График функции y = x2 называется параболой.

Свойства функции у = х2.


1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) - начало координат.

2. Если х ≠ 0, то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = х2 является промежуток [0; + ∞).
4. Если значения аргумента отличают­ся только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х2 - четная 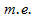при смене знак у аргумента с плюса на минус чётная степень также даёт плюс)
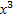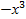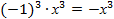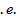* - нечетная функция, например, функция у= – нечетная, т.к. у= = ,т при смене у аргумента плюса на минус, минус выносится из под знака функции.
.
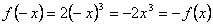5. На промежутке [0; + ∞) функция у = х2 возрастает.
6. На промежутке (-∞; 0] функция у = х2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
3.Фунуция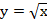
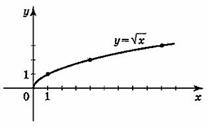
Область определения этой функции - промежуток [0;+∞), т. е. все неотрицательные числа.
Придавая переменной х несколько значений из области определения функции и вычисляя соответст­вующие значения у по формуле у= 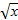., изображаем график функции.


Свойства функции у= .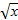
1. Если х = 0, то у = 0, т.е. график функции имеет с осями коорди­нат общую точку (0; 0) - начало координат.
2. Если х > 0, то у > 0, т.е. все точки графика функции, кроме на­чала координат, лежат над осью абсцисс.
3. Множеством значений функции у= 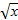. является промежуток [0;+∞).
4. Функция у= 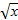. не является ни четной, ни нечетной.
5. Функция у= 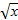. возрастающая в области определения.
6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.


4. Функция y = x3
Область определения этой функции - множество R действитель­ных чисел. Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х3, изображаем график функции.


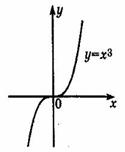
График функции у= х3 называется кубической параболой.


Свойства функции y = x3.

1. Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) - начале координат.
2. Если х > 0, то у > 0, а если х < 0, то у < 0, т.е. кубическая парабола лежит в пер­вом и третьем координатном углах.
3. Множеством значений функции у = х3 является вся числовая прямая.
4. Если значения аргумента отлича­ются только знаком, то и значения функции отличаются только знаком, т.е. кубическая парабола симметрична относительно начала координат (функция у = х3 - нечетная).
4. Функция у = х3 возрастающая в об­ласти определения.


5. Функция y = |x|
Область определения этой функции - множество R действитель­ных чисел.
Пользуясь определением модуля числа х при х > О получим у = х, а при х <0 получим у = - х. Таким образом, имеем:

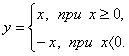
График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х < 0.

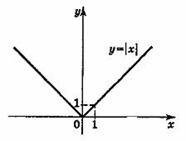
Свойства функции y =|x|
1. Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) - начале координат.
2. Если х ≠ 0, то у > 0, т.е. все точки графика функции y = |x|, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции y = |x| является промежуток [0;+∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| - четная).
5. На промежутке [0;+∞) функция y = |x| возрастает.
6. На промежутке (-∞;0] функция y = |x| убывает.
7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.

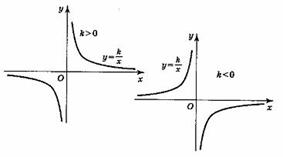
6. Функция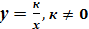
Область определения функции: .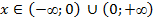
Область значений функции: y ..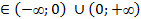
График — гипербола.
1. Нули функции. у ≠ 0, нулей нет.
2. Промежутки знакопостоянства,
Если k > 0, то у > 0 при х > 0; у < 0 при х < О.
Если k < 0, то у < 0 при х > 0; у > 0 при х < 0.
3. Промежутки возрастания и убывания.
Если k > 0, то функция убывает при ..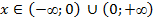
Если k < 0, то функция возрастает при ..
4. Четность (нечетность) функции.
Функция нечетная.

Квадратный трехчлен

Уравнение вида ax2+bx+c = 0, где a, b и с — некоторые числа, причем а≠0, называется квадратным.
В квадратном уравнении ax2+bx+c = 0 ко­эффициент а называется первым коэффициентом, b — вторым коэффициентам, с — свободным чле­ном.
Формула корней квадратного уравнения име­ет вид:
.
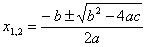Выражение 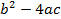называется дискриминан­том квадратного уравнения и обозначается через D.
Если D = 0, то существует только одно чи­сло, удовлетворяющее уравнению ax2+bx+c = 0. Однако условились говорить, что в этом случае ква­дратное уравнение имеет два равных действитель­ных корня, а само число - 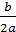называют двукрат­ным корнем.
Если D < 0, то квадратное уравнение не имеет действительных корней.
Если D > 0, то квадратное уравнение имеет два различных действительных корня.
Пусть дано квадратное уравнение ax2+bx+c = 0. Так как а≠0, то, разделив обе части данного уравнения на а, получим уравнение 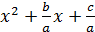. Полагая 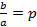и 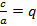, приходим к уравнению 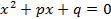, в котором первый коэффициент равен 1. Такое уравнение называется приведенным.
Формула корней приведенного квадратного уравнения имеет вид:
.
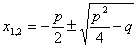Уравнения вида
аx2 +bx = 0, ax2 + с =0, аx2 = 0
называются неполными квадратными уравнениями.Неполные квадратные уравнения решаются разложением левой части уравнения на множители.


Дата добавления: 2016-06-05; просмотров: 1868;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.012 сек.