Структурный фактор базиса

Интенсивность различных отражений зависит от состава элементарной ячейки, то есть от числа и расположения атомов в ячейке (базис). Волны, рассеянные на разных атомах базиса будут складываться с разными фазами в зависимости от положения атома. Схема учета вкладов в амплитуду вектора 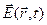дифрагированного луча такая же, как и при расчете дифракционной картины трехмерного кристалла, только суммирование надо будет проводить по всем атомам базиса, а не узлам кристаллической решетки.

Пусть базис содержит несколько атомов. Положение j –го атома ячейки (рис. 2.7) определяется радиус вектором 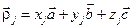, который проведен из узла решетки (рис.)

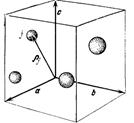
Рис.2.7 Положение j –го атома в элементарной ячейке

Этот узел жестко связан с рассматриваемой ячейкой, которую обозначим mnp. Выберем начало координат в узле 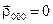. Относительно этого начала координат положение j –го атома в ячейке mnp определяется 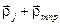. Распределение электронов в кристалле можно описать с помощью суперпозиции функций электронной плотности, каждая из которых связана с отдельным атомом. Концентрация электронов в точке 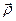вблизи j-го атома ячейки mnp определяется функцией электронной плотности 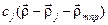. Полная электронная плотность 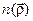в кристалле можно записать в виде суммы:

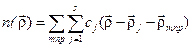, где первое суммирование (j=1, …, s) производится по всем атомам базиса, а второе – по всем узлам решетки, число которых равно М³ .

В соответствие с () общую амплитуду рассеяния в кристалле для вектора рассеяния 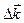можно записать в виде:

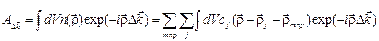(4545)

Вклад в А единичного члена 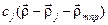в выражении (4545) равен:

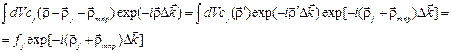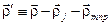где и 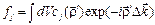- атомный фактор рассеяния.Более подробно атомный фактор рассеяния будет рассмотрен в п.2.6.

Выражение для амплитуды рассеяния можно записать следующим образом:

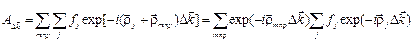(4646)

Так как сумма 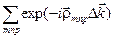не равна нулю только тогда, когда 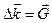, то в формуле (4646) вектор рассеяния 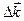можно заменить на вектор обратной решетки 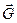. Сумма

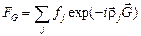называется структурным фактором рассеяния.

Произвольное отражение является отражением (hkl), когда вектор обратной решетки равен 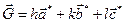. Для этого отражения, используя выражение 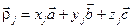, получаем:

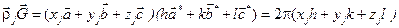
Структурный фактор для отражения (hkl) можно записать:

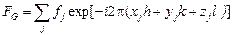
Структурный фактор не всегда является вещественной величиной;в значении интенсивности рассеянной волны входит F^*F, где F^* – величина, комплексно сопряженная F. Структурный фактор может уничтожать некоторые отражения, которые разрешены пространственной решеткой, и эти недостающие отражения помогают определить структуру. Это происходит в том случае, когда F равен нулю, тогда интенсивность отражения, определяемого вектором 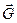и разрешенного решеткой, равна нулю.

Примеры: Структурный фактор ОЦК решетки.

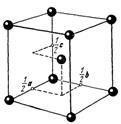
Рис. 2.8. ОЦК решетка

Базис ОЦК решетки состоит из двух одинаковых атомов (j=1,2). Координаты атомов в обычной элементарной кубической ячейке:

для j=1 [000]

для j=2 [½ ½ ½]

Тогд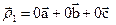а , а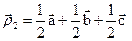

Структурный фактор рассеяния в данном случае равен:

,

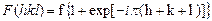где f – рассеивающая способность отдельного атома.

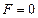, если сумма h+k+l равна нечетному целому числу;

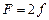, если сумма равна четному целому числу.

Рассмотрим структуру типа Na (натрий), который имеет ОЦК решетку. В дифракционной картине металлического натрия отсутствуют отражения, обусловленные плоскостями (100), (300), (111), (221), как видно сумма h+k+l равна нечетному целому числу. Однако отражения, определяемые плоскостями (200), (110) и (222), сумма равна четному целому числу, присутствуют. Указанные индексы плоскостей соответствуют кубической ячейке.

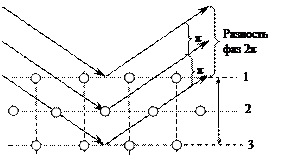
Физический смысл отсутствия отражения (100) в дифракционной картине для ОЦК решетки показан на рисунке 2.9. Отражение (100) обычно имеется тогда, когда лучи, отраженные от первой и третьей плоскостей на рис.2.30 имеют разность фаз 2π. Эти плоскости ограничивают элементарный куб. В объемно-центрированной кубической решетке имеется дополнительная промежуточная атомная плоскость, обозначенная на рисунке цифрой 2, рассеивающая способность которой такая же, как и у плоскостей 1 и 3. Но так как эта плоскость расположена посередине между ними, отраженный от нее луч сдвинут по фазе относительно луча, отраженного первой плоскостью, на π радианов, вследствие чего отражение от нее гасит отражение от первой плоскости. Гашение отражения (100) в ОЦК решетке происходит потому, что плоскости (100) состоят из одинаковых атомов.

Рис. 2.9. Схема, поясняющая отсутствие отражения (100) на дифракционной картине для ОЦК решетки. 1, 2, 3 – рассеивающие атомные плоскости. Разность фаз для лучей, отраженных от двух соседних плоскостей, равна π, так что амплитуда отражения от двух соседних плоскостей равна .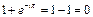

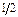
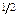
Рассмотрим теперь структуру типа цезий-хлор (рис.2.10), имеющую кубическую ячейку с базисом из двух атомов с координатами 000 – дляCs и 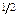- для Сl. В структуре CsCl(рис.1.26) такого гашения не будет: плоскости ионов Cs и Clчередуются, но рассеивающая способность ионов Csзначительно больше рассеивающей способности ионов Cl, так как Cs⁺ имеет 54 электрона, а Cl^-- только 18.

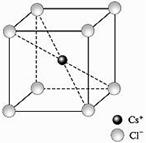
Рис.2.10. Кристаллическая структура хлористого цезия.

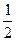
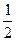
Пространственной решеткой является простая кубическая решетка, а базис состоит из иона Cs⁺с координатами 000 и иона Cl^-с координатами 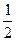.Структурный фактор кубической ячейки CsCl, вычисляемый по формуле ( ), окажется равным:

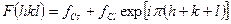
F(hkl) не будет равен нулю ни при четной, ни при нечетной сумме индексов. В самом деле, теперь атомы расположенные в центре и по углам элементарной ячейки - разные, следовательно и рассеивают волны они по-разному 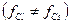. Структурный фактор окажется либо суммой, либо разностью неравных величин 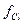и 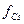. Если теперь рассмотреть, как в случае ОЦК решетки, плоскости типа 1 и 2 на рис.2.9, то видно, что они уже разные - содержат разные атомы и будут давать разный по величине вклад в амплитуду рассеяния или одного или противоположного знака. Сумма вкладов не будет равной нулю. Поэтому узлам обратной решетки с четной суммой индексов (когда вклады атомов хлора и цезия складываются), например (200), будут соответствовать сильные дифракционные максимумы (кружочки) а нечетной сумме индексов (когда вклады атомов хлора и цезия вычитаются), например (100), - слабые дифракционные максимумы. По расположению узлов в обратной решетке тогда можно определить период решетки, а по чередованию "ярких" и "слабых" узлов - определить положение атомов в базисе решетки.