Атомный фактор рассеяния

В п. 2.5 было получено выражение для атомного фактора рассеяния:

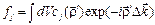
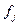- мера рассеивающей способности j-го атома элемента.

Величина f зависит от числа и распределения электронов атома, а также от длины волны и угла рассеяния излучения.

Произведем расчет фактора рассеяния в рамках классических представлений.

Излучение, рассеянное единичным атомом, должно учесть интерференционные эффекты внутри атома. Выше (см. формулу…)

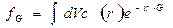
интегрирование осуществляется в пределах электронной плотности 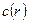, связанной с единичным атомом. Назовем величину f атомным фактором рассеянияили форм-фактором. Пусть 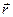образует угол α с 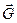; тогда 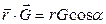. Если распределение электронной плотности обладает сферической симметрией относительно начала координат, то

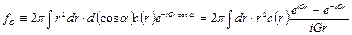
где мы проинтегрировали по 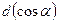в пределах от -1 до 1. Таким образом, величина атомного фактора рассеяния определяется выражением:

(***)

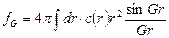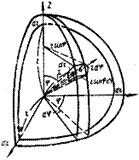
Рис. 2.11. К вычислению разности хода лучей, рассеянных объемом dvпо отношению к началу координат О, находящемуся в центре атома.

К выводу формулы (***). Распределение электронной плотности обладает сферической симметрией относительно начала координат, находящемуся в центре атома (рис. 2.11).

Если тот же самый электронный заряд был бы сконцентрирован в начале координат, где 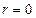, то в интеграле выражения (2.65) только произведение 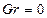должно было бы вносить вклад в подинтегральное выражение. В этом предельном случае 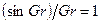, и для всех G

,

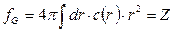где Z – число электронов в атоме. Поэтому 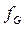- это отношение амплитуды излучения, рассеянного реальным распределением электронов в атоме, к амплитуде излучения, рассеянного одним электроном, расположенным в точке.

Полное распределение электронов в твердом теле очень близко к распределению электронов в соответствующих свободных атомах. Это утверждение не означает, что электроны, наиболее удаленные от ядра, или валентные электроны не перераспределяются при образовании твердого тела; это означает лишь то, что интенсивности отражений рентгеновских лучей хорошо описываются величинами форм-факторов свободных атомов.