Температурная зависимость линий отражения.

Рассмотрим выражения для амплитуды излучения, рассеянного кристаллом:

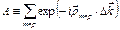
Пусть положение атома в момент времени t задано выражением:

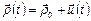где 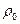отвечает равновесному положению атома, 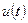- величина, изменяющаяся во времени. (Колебания каждого атома около своего положения равновесия происходят независимо).

Тогда среднее значение амплитуды рассеянной волны (формула (2.59в)) в направлении дифракционного максимума можно записать так:

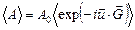
где 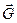– вектор, равный изменению волнового вектора при отражении, и 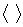означает среднее при тепловом равновесии. Наличие множителя А₀ обусловливает то, что все дифракционные линии будут четкими.

Экспоненциальный множитель в (2.68) уменьшает интенсивность. Разложим экспоненциальный множитель в ряд:

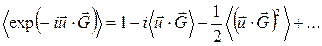
Но 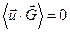, так как 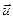соответствует хаотическому тепловому движению, не скоррелированному с направлением .

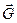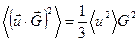
Множитель 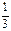появляется в результате геометрического усреднения по трем направлениям, так как нас интересует только компонента u вдоль направления G.

Функция 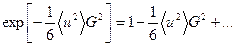до первых двух членов совпадает с функцией 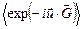. Поэтому заменим на .

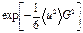Таким образом, интенсивность рассеянной волны, равная квадрату амплитуды, есть

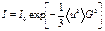(2.72)

где 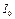- ранее полученная нами интенсивность излучения, рассеянного неподвижной решеткой.

Экспоненциальный множитель 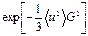- множитель Дебая – Валлера.

Здесь 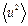- среднеквадратичное смещение атома. Среднее значение потенциальной энергии 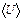классического гармонического осциллятора в трех измерениях при тепловом равновесии равно 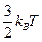, откуда

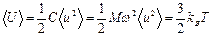
где С – силовая постоянная, М – масса атома и ω – частота осциллятора. Мы использовали здесь равенство .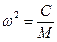

Таким образом, интенсивность рассеянного излучения равна

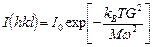
где h, k, l - индексы в выражении 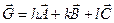. Этот классический результат является хорошим приближением при высоких температурах.

Для квантовых осцилляторов 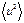не равно нулю даже при 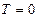вследствие нулевых колебаний. Мы продолжаем использовать модель независимого гармонического осциллятора для характеристики движения (колебания) атома: при температуре абсолютного нуля это движение можно описать через нулевую энергию 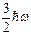. Это энергия трехмерного квантового гармонического осциллятора в его основном состоянии, отнесенная к величине классической энергии того же осциллятора, находящегося в покое. Половина энергии осциллятора есть потенциальная энергия, так что выражение (2.73) дает для средней потенциальной энергии в основном состоянии:

,

,

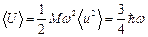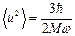откуда, используя (2.72), получаем при Т = 0:

.

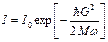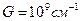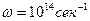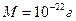Если , и , то показатель экспоненты равен приблизительно 0,1, так что 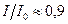. В этом случае при абсолютном нуле 90% пучка испытывает упругое рассеяние, а 10% - неупругое рассеяние. Энергия, потерянная при неупругом рассеянии рентгеновского пучка, переходит к атому, который переходит при этом в возбужденное излучательное состояние.

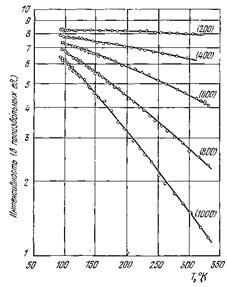
Рис.2.12. Температурная зависимость интенсивности дифракционных максимумов (h00) для алюминия. Отражения (h00) с нечетными значениями h запрещены в ГЦК структуре

Из выражения (2.74) и из рис. 2.34 видно, что интенсивность дифракционной линии уменьшается (хотя и не очень резко) с ростом температуры. На отражениях, соответствующих малым значениям G, это уменьшение менее заметно, чем на отражениях, которым соответствуют большие значения G. Мы рассчитали интенсивность рассеянных пучков при когерентной дифракции или при упругом рассеянии по строго определенным, полученным из условий Брэгга направлениям.

При данной температуре множитель Дебая-Уоллера дифракционной линии уменьшается с увеличением величины вектора обратной решетки 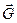, связанного с отражением. Чем больше 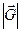, тем слабее будет отражение при высоких температурах. Температурная зависимость интенсивности отраженного излучения для отражений (h00) в алюминии показана на рисунке 2.12.

<2 3 456 7 8 >

Дата добавления: 2021-05-28; просмотров: 340;