Учет распределения потоков тепловых нейтронов в гетерогенных ячейках
Если гетерогенность среды существенна (шаг ячейки порядка длины свободного пробега нейтронов или больше), некоторые усредненные физические характеристики следует вычислять с учетом распределения тепловых нейтронов внутри ячейки (микрораспределения). Для расчета микрораспределения нейтронов ячейка разбивается на концентрические зоны. Мы это сделали в пункте 4. Нас будут интересовать средние значения нейтронного потока в каждой из этих зон.
Вообще говоря, для расчета распределения нейтронов в ячейке следовало бы использовать более строгую, чем обычное диффузионное приближение, теорию переноса, так как условия применимости диффузионной теории в зонах ячейки, как правило, не выполняются из-за малости зон, а в блоке, кроме того, из-за большого поглощения нейтронов. Однако, благодаря относительной простоте, диффузионную теорию часто применяют, и она дает качественно верные результаты. Неточность ее проявляется в том, что распределение нейтронов получается более плавным, нежели в действительности. Мы ограничимся диффузионным приближением.
Вначале необходимо определить макроскопические сечения Σa и Σtr отдельно в каждой зоне ячейки, пользуясь найденными ранее микроскопическими усредненными сечениями σa и σtr и формулами:
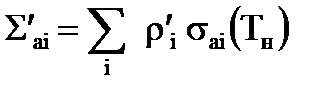 ;
; 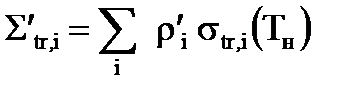
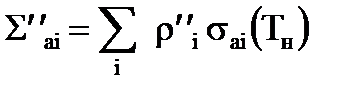 ;
; 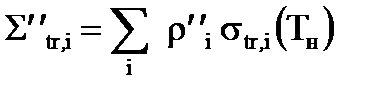
Кроме сечений необходимо получить для гомогенизированной ячейки коэффициент диффузии D и длину диффузии L:
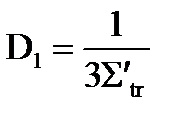 ,
, 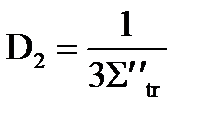 ;
;
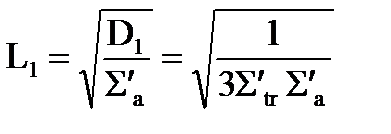 ,
, 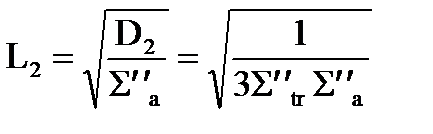 .
.
Будем считать, что источники тепловых нейтронов распределены в каждой зоне ячейки равномерно и мощность их пропорциональна замедляющей способности зон. Мощность источников во второй зоне ячейки можно принять за единицу, тогда в первой зоне она будет равна
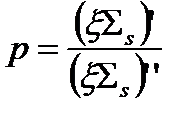
Величину в каждой зоне вычисляют по формуле
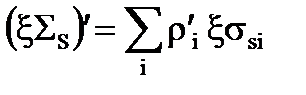 ;
; 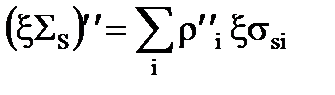
В диффузионном приближении формулы для средних нейтронных потоков в первой и второй зоне ячейки имеют вид:
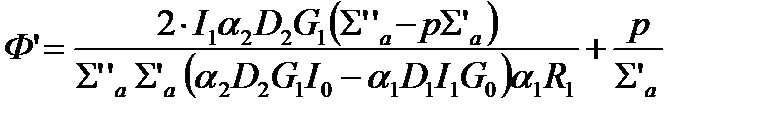
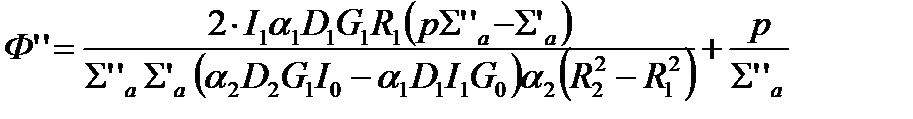
где D1 и D2 – коэффициенты диффузии тепловых нейтронов: 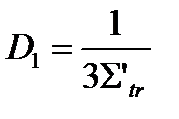 ,
, 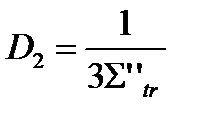 ;
;
α1 и α2 – величины. Обратные длинам диффузии: 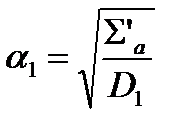 ,
, 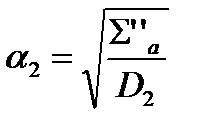 ;
;
R1 и R2 – эквивалентные радиусы зон: 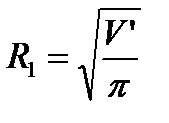 ,
, 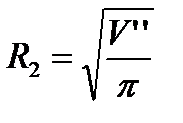 ;
;
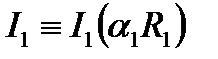 ,
, 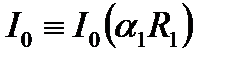 ;
;
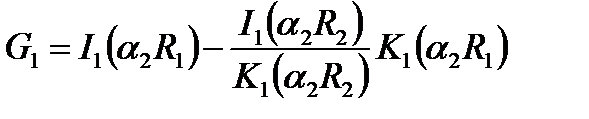 и
и 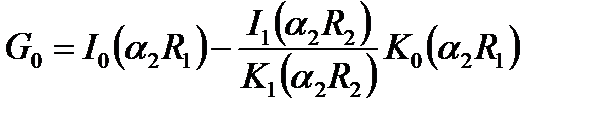 .
.
In, Kn – функции Бесселя мнимого аргумента. Эти функции можно посчитать в Mathcad или MS Excel с помощью специальных операций (см. приложение).
В дальнейшем мы будем использовать только отношение 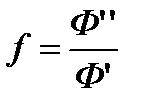 . Если оно близко к 1, то эффект гетерогенности не существен.
. Если оно близко к 1, то эффект гетерогенности не существен.
Если f заметно отличается от 1. то при расчете средних по ячейке параметров необходимо усреднять их не только с учетом объемов зон, но и потоков в них:
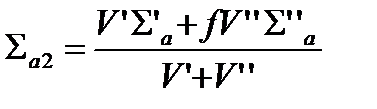
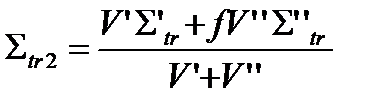
и, следовательно 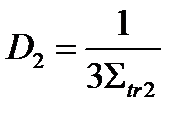 и
и 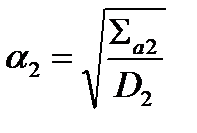 .
.
Дата добавления: 2021-05-28; просмотров: 643;











