Сходящиеся и ограниченные последовательности.

Определение: Последовательность называется сходящейся, если она имеет конечный предел.

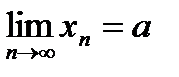- число.

В противном случае последовательность называется расходящейся.

Определение: Последовательность {x_n} называется ограниченной сверху, если существует число M такое, что для всех членов последовательности x_n 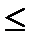M.

Определение: Последовательность {x_n} называется ограниченной снизу, если существует число m такое, что для всех членов x_n³m.

Определение: Последовательность называется ограниченной, если она ограниченна сверху и снизу, т.е. $ число A>0 такое, что для всех членов последовательности |x_n|£A.

Бесконечно малые и бесконечно большие последовательности.

Связь между ними.

Определение: Последовательность {x_n} называется бесконечно малой, если для любого, сколь угодно малого, положительного числа e, найдется номер последовательности N, зависящий от 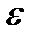, начиная с которого выполняется неравенство |x_n|<e.

.

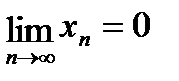Определение: Последовательность {x_n} называется бесконечно большой, для любого, сколь угодно большого, положительного числа А, найдется номер последовательности N, начиная с которого выполняется неравенство |x_n|>A.

.

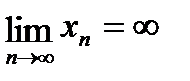Теорема: Бесконечно малые (б/м) и бесконечно большие (б/б) последовательности взаимообратные.

Док-во:

1) б/б есть обратная величина для б/м.

Пусть {x_n} – б/м при n®¥. По определению: " 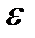> $N: "n>N Þ |x_n|<e.

Перейдем к обратным величинам: 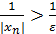. Обозначим 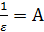. Если e – б/м, то А – б/б. Тогда 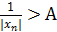, что означает из определения, что 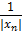– б/б.

2) б/м есть обратная величина для б/б.

Пусть {x_n} ‒ б/б при n®¥. По определению: "A>0 $N: "n>N Þ |x_n| > A.

Перейдем к обратным величинам: 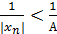. Обозначим 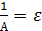. Если А – б/б, то e – б/м. Тогда 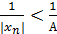, что означает из определения, что 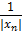‒ б/м.

Ч.т.д.