Ограниченные и неограниченные функции. Монотонные функции
Определение 1. Функция 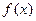 , заданная на множестве Х, называется ограниченной сверху на этом множестве, если существует число М, такое, что
, заданная на множестве Х, называется ограниченной сверху на этом множестве, если существует число М, такое, что 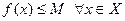 . Функция
. Функция 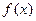 , заданная на множестве Х, называется ограниченной снизу на этом множестве, если существует число М, такое, что
, заданная на множестве Х, называется ограниченной снизу на этом множестве, если существует число М, такое, что 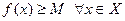 . Функция
. Функция 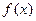 , заданная на множестве Х, называется ограниченной на этом множестве, если существуют числа
, заданная на множестве Х, называется ограниченной на этом множестве, если существуют числа 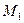 и
и 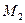 , такие, что
, такие, что 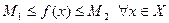 .
.
Иными словами, функция 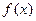 ограничена на множестве Х, если на этом множестве она ограничена и сверху, и снизу.
ограничена на множестве Х, если на этом множестве она ограничена и сверху, и снизу.
Например, функция 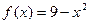 ограничена сверху на множестве R, так как
ограничена сверху на множестве R, так как 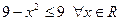 , функция
, функция 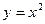 ограничена снизу на R, так как
ограничена снизу на R, так как 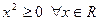 , функция
, функция 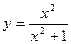 ограничена на R, так как
ограничена на R, так как 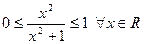 . Ограниченными являются также функции
. Ограниченными являются также функции 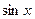 и
и 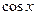 , так как
, так как 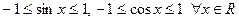 .
.
Свойства ограниченных функций:
1) если функции f и g ограничены на множестве Х, то и функции 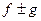 и
и 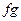 тоже ограничены на множестве Х;
тоже ограничены на множестве Х;
2) если функция 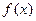 ограничена сверху, то функция
ограничена сверху, то функция 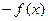 ограничена снизу;
ограничена снизу;
3) если функция 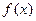 положительна на множестве Х и ограничена на нем снизу положительным числом, то функция
положительна на множестве Х и ограничена на нем снизу положительным числом, то функция 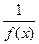 ограничена на Х.
ограничена на Х.
Доказательство. 1) В силу ограниченности функций f и g на множестве Х найдутся числа 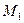 и
и 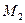 ,
, 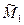 и
и 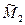 , такие, что
, такие, что 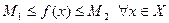 и
и 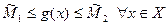 . А тогда
. А тогда 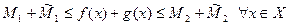 и
и 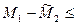
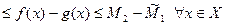
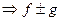 - ограниченные на Х функции. Чтобы доказать ограниченность функции
- ограниченные на Х функции. Чтобы доказать ограниченность функции 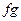 , положим
, положим 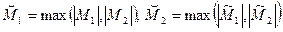 . Тогда имеют место неравенства
. Тогда имеют место неравенства 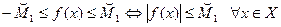 и
и 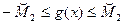
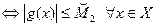 , из которых следует, что
, из которых следует, что 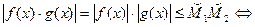
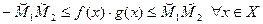 , а это и означает ограниченность функции
, а это и означает ограниченность функции 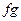 .
.
2) В силу ограниченности функции f сверху найдется число М, такое, что 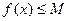 . Тогда
. Тогда 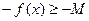 , что и означает ограниченность функции
, что и означает ограниченность функции 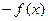 снизу.
снизу.
3) По условию 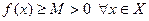 , поэтому
, поэтому 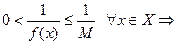 ограниченность функции
ограниченность функции 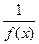 .
.
Например, функция 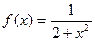 ограничена на множестве R действительных чисел, так как
ограничена на множестве R действительных чисел, так как 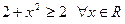 .
.
Чтобы дать определение неограниченной сверху или снизу функции, нужно сформулировать отрицание соответствующей части определения 1.
Определение 2. Функция 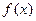 называется неограниченной сверху на множестве Х, если не существует числа М, такого, что
называется неограниченной сверху на множестве Х, если не существует числа М, такого, что 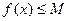 для любого
для любого 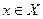 , то есть для любого числа М найдется число
, то есть для любого числа М найдется число 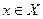 , такое, что
, такое, что 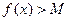 .
.
Функция 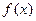 называется неограниченной снизу на множестве Х, если для любого числа М найдется число
называется неограниченной снизу на множестве Х, если для любого числа М найдется число 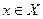 , такое, что
, такое, что 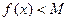 .
.
Докажем, например, что функция 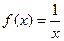 неограниченна на множестве
неограниченна на множестве 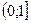 сверху. Возьмем произвольное число
сверху. Возьмем произвольное число 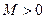 и покажем, что
и покажем, что 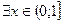 , такое, что
, такое, что 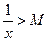 .
.
Для этого, очевидно, достаточно взять 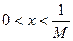 , например,
, например, 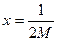 .
.
Если функция 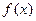 ограничена на множестве Х, то множество
ограничена на множестве Х, то множество 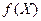 ограничено, поэтому имеет точную верхнюю и точную нижнюю границы. Их обозначают
ограничено, поэтому имеет точную верхнюю и точную нижнюю границы. Их обозначают 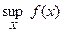 и
и 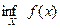 соответственно и называют точной верхней границей и точной нижней границей функции
соответственно и называют точной верхней границей и точной нижней границей функции 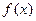 на множестве Х.
на множестве Х.
Определение 3. а) Функция 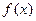 называется возрастающей на множестве Х, если большему значению аргумента соответствует большее значение функции, т.е.
называется возрастающей на множестве Х, если большему значению аргумента соответствует большее значение функции, т.е. 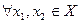 , таких, что
, таких, что 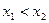 , имеем
, имеем 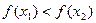 .
.
б) Функция 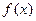 называется убывающей на множестве Х, если
называется убывающей на множестве Х, если 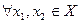
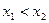
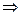
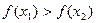 .
.
в) Функция 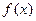 называется неубывающей на множестве Х, если
называется неубывающей на множестве Х, если 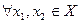
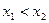
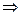
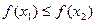 .
.
г) Функция 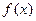 называется невозрастающей на множестве Х, если
называется невозрастающей на множестве Х, если 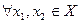
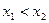
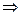
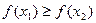 .
.
Возрастающие, убывающие, неубывающие, невозрастающие функции называются монотонными, возрастающие и убывающие – строго монотонными функциями.
При исследовании функций на монотонность полезны следующие утверждения.
Теорема. а) Если функции f и g возрастают (убывают) на множестве Х, то и функция f+g возрастает (убывает) на Х.
б) Если 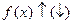 на множестве Х, то
на множестве Х, то 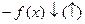 на Х.
на Х.
в) Если функции f и g неотрицательны на множестве Х и возрастают (убывают) на этом множестве, то их произведение 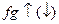 на Х.
на Х.
г) Если функция f положительна на множестве Х и возрастает (убывает), то 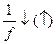 на Х.
на Х.
д) Если функция 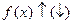 на множестве Х, а функция
на множестве Х, а функция 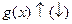 на множестве
на множестве 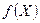 , то функция
, то функция 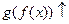 на множестве Х.
на множестве Х.
Доказательство. Докажем, например, а) и д).
а) Пусть функции f и g возрастают на множестве Х и 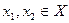 , причем
, причем 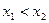 . Тогда
. Тогда 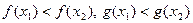 и поскольку неравенства одинакового смысла можно складывать, то
и поскольку неравенства одинакового смысла можно складывать, то 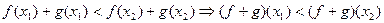 , т.е. функция f+g возрастает.
, т.е. функция f+g возрастает.
д) Пусть функция 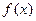 убывает на множестве Х, а функция
убывает на множестве Х, а функция 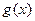 убывает на множестве
убывает на множестве 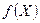 ,
, 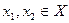 , причем
, причем 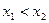 . Тогда
. Тогда 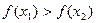 и, так как
и, так как 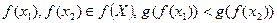 , т.е. функция
, т.е. функция 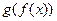 возрастает на множестве Х.
возрастает на множестве Х.
Остальные утверждения теоремы доказать самостоятельно.
Теорема доказана.
Отметим, что прибавление постоянной величины к функции и умножение функции на положительную постоянную величину не меняет характера монотонности.
Пример. Докажем, что функции 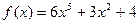 и
и 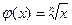 возрастают на промежутке
возрастают на промежутке 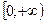 .
.
Доказательство. Функция 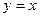 возрастает на промежутке
возрастает на промежутке 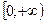 . Тогда по свойству в)
. Тогда по свойству в) 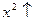 и
и 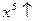 на
на 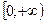 ,
, 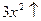 и
и 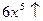 , поэтому по свойству а) возрастает и функция
, поэтому по свойству а) возрастает и функция 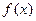 .
.
Для функции 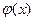 доказательство проведем методом от противного. Пусть
доказательство проведем методом от противного. Пусть 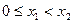 . Предположим противное, т.е. что
. Предположим противное, т.е. что 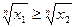 . Тогда, в силу возрастания функции
. Тогда, в силу возрастания функции 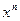 ,
, 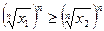 , т.е.
, т.е. 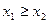 , что противоречит неравенству
, что противоречит неравенству 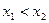 . Из полученного противоречия следует, что
. Из полученного противоречия следует, что 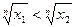 , т.е. функция
, т.е. функция 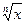 возрастает на промежутке
возрастает на промежутке 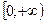 .
.
Дата добавления: 2016-06-09; просмотров: 28043;











