Аффинные (косоугольные) координатные системы.

В отличие от описанных выше декартовых координатных систем в косоугольных координатных системах координатные плоскости и координатные линии не являются перпендикулярными друг другу. Это обстоятельство затрудняет аналитическое разложение радиус-вектора по координатным направлениям и порождает возможность нескольких способов описания векторной величины. Косоугольные координатные системы являются простейшим обобщением декартовых координатных систем, а приёмы их применения в практических расчётах, в частности, в кристаллографии, оказываются полезными и при использовании общих, в частности, ортогональных, криволинейных координатных систем.

Пусть координатные направления рассматриваемой правой косоугольной системы координат заданы исходными векторами 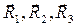(рисунок 1). Пусть векторы 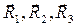имеют разную длину, но одинаковую физическую размерность – размерность длины. Пусть необходимо произвольный радиус-вектор 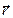разложить на составляющие, параллельные координатным направлениям. Геометрический метод параллельного проектирования позволяет выполнить требуемое построение, но при этом возникают трудности аналитического расчёта и не в полной мере выявляется совокупность возможностей описания векторной величины. В этом плане алгебраический подход является более предпочтительным.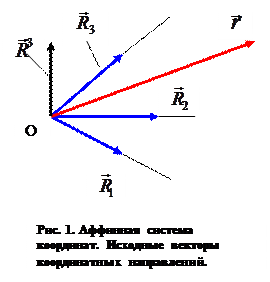

Итак, необходимо получить разложение произвольного радиус-вектора 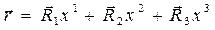. (1)

В разложении (1) коэффициенты разложения 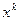записаны с верхними индексами, удобство принятого обозначения мы оценим ниже. В силу того, что векторы 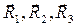не являются ортогональными друг другу, может иметь место соотношение (хотя бы для некоторых значений индексов)

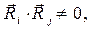
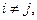
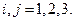(2)

В этом случае скалярное произведение вектора 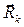на радиус-вектор 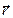формально может содержать все коэффициенты искомого разложения:

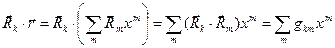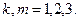, (3)

Если 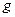- определитель (детерминант) матрицы 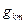- не равен нулю, т.е. матрица 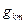не является особенной: 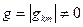, то решение линейной системы уравнений (3) можно записать в форме:

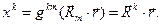(4)

В соотношениях (3)-(4) использованы обозначения

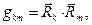
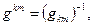
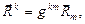
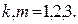(5)

По повторяющимся индексам (один раз – верхнее положение, другой – нижнее) предполагается суммирование от 1 до 3 (правило Эйнштейна). Обозначение 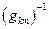- общепринятое обозначение обратной матрицы по отношению к исходной. Векторы 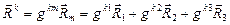являются при этом специфической комбинацией направляющих векторов исходной косоугольной системы координат.

Формально проблема разложения произвольного радиус-вектора решена: найдены коэффициенты разложения (1). Но за этими «сухими» математическими формулами трудно разглядеть геометрическое содержание проделанных операций. Поэтому сделаем следующее. Введём векторы 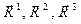с помощью определений:

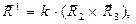
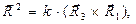
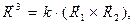(6)

где k - некоторая постоянная величина. Основное свойство введённой тройки векторов заключается в том, что каждый из них перпендикулярен двум направляющим векторам с отличным значением индекса исходной системы косоугольных координат, что влечёт за собой выполнение условий

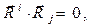
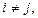
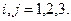(7)

Потребуем дополнительно, чтобы выполнялись условия

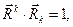
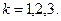(8)

Условия (8) должны быть выполнены для каждого значения индекса отдельно:

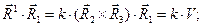
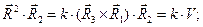(9)

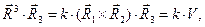
где 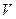- объём параллелепипеда, построенного на направляющих векторах 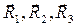исходной системы координат. Условия (8) будут выполнены, если величину 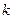положить равной 1/V:

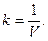(10)

Направляющие векторы с верхним расположением индекса 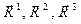определяют систему косоугольных координат, которую называют взаимной системой координат по отношению к исходной системе. Легко проверяется, что если исходная система косоугольных координат была правой системой (т.е. V>0), то взаимная система координат тоже будет правой:

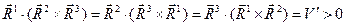, (11)

более того, оказывается, что величины 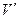и 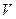связаны между собой зависимостью

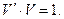(12)

Если ввести в рассмотрение объект с двумя верхними индексами

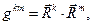(13)

то можно обнаружить, что матрица 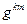является обратной матрицей по отношению к матрице :

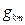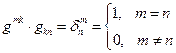(14)

и выполняются соотношения

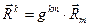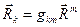; . (15)

В соответствии с соотношениями (15) от составляющих вектора с нижним индексом можно перейти к составляющим вектора с верхним индексом и далее вернуться к исходным составляющим:

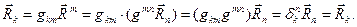(16)

Обратим внимание читателя на то, что взаимная косоугольная система координат очень строго организована: единственным, специфическим образом выбраны новые координатные направления и, кроме того, величины направляющих векторов новых направлений и даже их физическая размерность определена в соответствии с зависимостями (6), (9).

Итак, поскольку имеют место соотношения

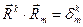, (17)

коэффициенты разложения радиус-вектора 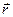в форме (1) можно получить скалярным умножением направляющего вектора взаимной системы координат на рассматриваемый радиус-вектор:

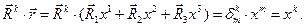(18)

Зависимость

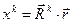(19)

формально совпадает с результатом (4), но наполнена обозримым геометрическим содержанием.

Условие ортогональности системы исходных направляющих векторов и направляющих векторов взаимной системы координат (17) позволяет получить разложение произвольного радиус-вектора по координатным направлениям взаимной системы координат:

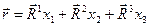. (20)

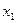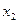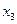Коэффициенты разложения , и определяются соотношениями

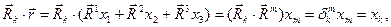
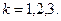(21)

Окончательно получаем

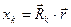. (22)

Коэффициенты разложения радиус-вектора 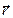по координатным направлениям исходной системы координат 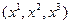называют «контравариантными» координатами радиус-вектора, а коэффициенты разложения радиус-вектора 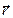по координатным направлениям взаимной системы координат 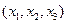называют «ковариантными» координатами радиус-вектора. Объект сложной структуры, рассматриваемый относительно произвольной системы координат, может иметь часть индексов в верхнем положении и часть в нижнем положении. В этом случае он является контравариантным по первой части индексов и ковариантным по второй части индексов. В тензорном исчислении определены операции подъёма и опускания индексов с помощью фундаментальных объектов 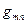и 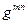. Они определены зависимостями (5) и (13), а примеры выполнения упомянутых операций содержатся в соотношениях (15).

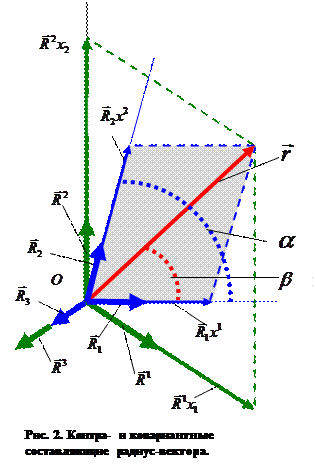Чтобы сделать различие контравариантных и ковариантных координат радиус-вектора более наглядным, рассмотрим частный случай косоугольной системы координат (рис. 2), в которой направление вектора 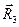перпендикулярно плоскости, в которой лежат векторы 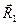и 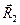и радиус-вектор 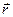. Пусть угол между векторам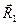и и 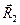равняется 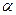, а угол между векторам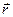и и 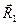равняется 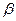. Декартовы координаты вектора 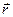суть: 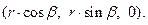Составляющие направляющих векторов 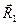, 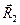и 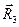в исходной системе декартовых координат:

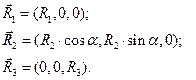Для рассматриваемого случая объём параллелепипеда, построенного на направляющих векторах исходной системы координат, равен

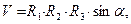(23)

где - модули соответствующих векторов. Пространственная ориентация направляющих векторов взаимной системы показана на рис. 2. Проекции направляющих векторов взаимной системы на оси исходной декартовой системы координат определены соотношениями:

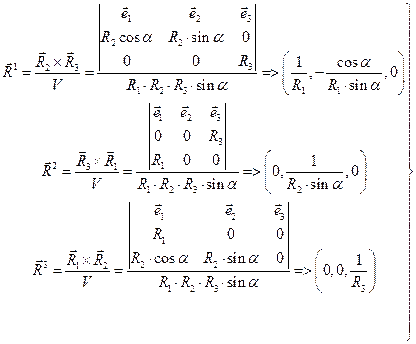, (24)

где ( ) – безразмерные орты исходной декартовой системы координат.

Модули направляющих векторов взаимной системы в соответствии с определениями последних в символической форме (6) равны

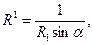
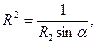
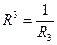. (25)

Заметим, что даже в рассматриваемом случае может оказаться 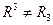, эти величины равны друг другу только тогда, когда выполнено условие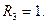

Для контравариантных координат радиус-вектора в соответствии с зависимостями (19), (6) и (10) получаем:

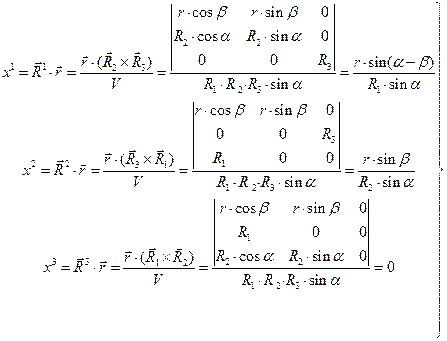(26)

Заметим, что приведённые выше результаты можно получить и вычислением скалярных произведений непосредственно, используя соотношения (25).

Ковариантные координаты радиус-вектора можно рассчитать с помощью соотношений (22):

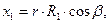
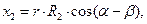
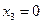. (27)

Обратим внимание читателя на то, что контравариантные и ковариантные координаты радиус-вектора различаются между собой не только величиной, но и размерностью. Заметим также, что и контравариантные и ковариантные составляющие радиус-вектора получаются в результате параллельного проектирования на соответствующие координатные направления. Встречающееся в учебной литературе утверждение, что ковариантные координаты можно получить перпендикулярным проектированием радиус-вектора на контравариантные координатные направления, справедливо только в том случае, если все модули направляющих векторов исходной косоугольной системы координат имеют единичную длину.