Формулы комбинаторики
Пример.Сколькими способами можно набрать семизначный номер телефона, если все его цифры различны. Очевидно, первую цифру можно набрать 10 способами, вторую - 9, так как одна цифра уже использована,..., седьмую - 4. Согласно правилу произведения общее число возможных номеров равно 10×9×8×7×6×5×4 = 604800.
Решение.Пусть из некоторого множества, состоящего из n различимых элементов, отбирается в определённом порядке m. Для подсчёта числа возможных вариантов заметим, что первый элемент можно выбрать n способами, второй - (n - 1), ..., m -й - (n - m + 1) способами. Согласно правилу произведения общее число вариантов будет равно n×(n - 1)×...×(n - m + 1). Такие комбинации называют размещениями, а число вариантов обозначают
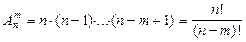
При n = m говорят о перестановках из n элементов, их число равно
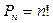 =1·2·....·(n-1)·n (n – факториал).
=1·2·....·(n-1)·n (n – факториал).
В частности, P0=0!=1, P1=1!=1, P2=2!=1·2=2, P3=1·2·3=6.
Если порядок отбираемых m элементов из n не играет роли, то говорят о числе сочетаний из n элементов по m. Поскольку
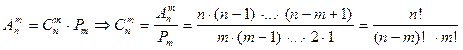 .
.
В частности, 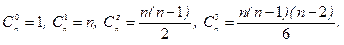
Пример.Сколькими способами можно из 20 присяжных заседателей отобрать трёх для участия в судебном процессе.
Решение. Поскольку несущественно, в каком порядке отобраны кандидатуры, число вариантов равно
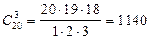 .
.
Пример.Сколькими способами из 20 членов правления фирмы можно отобрать трёх для замещения вакансий вице-президентов, отвечающих, соответственно, за производство, финансы, реализацию продукции?
Решение. Поскольку порядок при таком выборе играет существенную роль, число вариантов равно
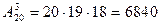
Замечание. При большом n подсчёт числа вариантов по этим формулам требует громоздких вычислений n!. В этом случае пользуются асимптотической формулой Стирлинга
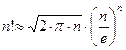 .
.
Пример.Среди K поставленных единиц данного товара L единиц не удовлетворяют предъявляемым условиям. Найти вероятность того, что среди k £ K отобранных для выборочного контроля качества единиц ровно l £ L не будут удовлетворять этим требованиям (этот опыт называется “контролем качества”).
Решение. Опыт заключается в случайном отборе k образцов. Следовательно, исходы этого испытания равновозможны и их общее число равно 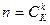 . Событие A состоит в том, что из k отобранных ровно l не будут удовлетворять этим требованиям. Число исходов, благоприятствующих A, согласно правилу произведения равно
. Событие A состоит в том, что из k отобранных ровно l не будут удовлетворять этим требованиям. Число исходов, благоприятствующих A, согласно правилу произведения равно 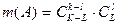 , здесь первый множитель даёт число вариантов отбора хороших, а второй - плохих образцов. Отсюда искомая вероятность
, здесь первый множитель даёт число вариантов отбора хороших, а второй - плохих образцов. Отсюда искомая вероятность 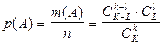 .
.
--
Дата добавления: 2017-01-08; просмотров: 2498;











