Геометрическая вероятность
Рассмотрим так называемую геометрическую схему теории вероятностей. Для этого рассмотрим опыт, состоящий в бросании случайным образом точки на отрезок [0, l], предполагая, что попадания в любую точку равновозможны. Пространство элементарных событий в этом эксперименте - все точки отрезка [0, l] –W. Поскольку множество элементарных событий несчётно (бесконечное) и все они равновозможны, то для любого w: p(w) = 0. То есть классическая схема неприменима. В этом случае припишем событию A - попаданию брошенной точки на отрезок [a, b], входящий в [0, l], - вероятность, пропорциональную его длине, то есть положим
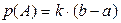 , (1.5)
, (1.5)
где (b – a) - длина отрезка. Коэффициент k найдём из условия нормировки
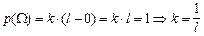 и
и 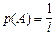 . (1.6)
. (1.6)
Легко убедиться в справедливости всех аксиом.
Естественно, что вместо отрезка можно говорить о плоской фигуре, определив вероятность как отношение
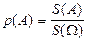 , (1.7)
, (1.7)
где S(A), S(W) - площади соответствующих фигур. Совершенно аналогично можно поступить и в трёхмерном (или большей размерности) случае.
Пример. В квадратном окне со стороной a имеется квадратная форточка со стороной b. Во время игры маленький мячик случайно попадает в окно. Какова вероятность того, что мяч через открытую форточку влетит в комнату, не разбив окна (событие А)? Какова вероятность, что окно разобьется (событие B)?
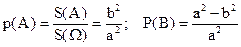 .
.
Дата добавления: 2017-01-08; просмотров: 2193;











