Дискретизация и квантование, характеристики АЦП и ЦАП.
В большинстве случаев информация о физических процессах и явлениях представляется в аналоговой форме. В аналоговой же форме часто должны формироваться и управляющие воздействия на различные объекты, подвергающиеся анализу, контролю или управлению. Для возможности осуществлять обработку полученной с датчиков аналоговой информации цифровыми методами необходимо выполнить преобразование этой информации к виду, доступному к «пониманию» цифровыми устройствами. Подобное преобразование называется аналого-цифровым. Обратное преобразование, заключающееся в переводе информации, полученной с выходов цифрового устройства к виду непрерывной функции времени или иного ее параметра, называется цифро-аналоговым. Соответственно устройства, выполняющие такие преобразования, называются аналого-цифровыми преобразователями (АЦП) и цифро-аналоговыми преобразователями (ЦАП).
Из рассмотренных ранее типов цифровых устройств очевидно, что входная информация для них должна характеризоваться дискретностью (конечным количеством) своих значений (кодов). Поскольку наиболее удобной формой представления информации для обработки средствами электронных устройств являются напряжения и токи, изменяющиеся во времени, то в качестве дискретных значений этих сигналов можно выбрать как дискретные значения времени, так и дискретные уровни напряжений или токов. На рис. 10.1,а представлена зависимость аналогового напряжения uа(t) в качестве информационного сигнала, получаемого от объекта с помощью некоторого первичного преобразователя (датчика). Исходный сигнал характеризуется непрерывностью значений как по времени, так и по уровню напряжения. Задав n равных промежутков времени Tд, можно выделить конечную последовательность импульсов с амплитудами uд(iTд), где i=1,n, точно соответствующими значениям напряжений uа(t) в эти моменты времени. Таким образом, реализуется свойство дискретности сигнала по времени. По уровню напряжения дискретизированный по времени сигнал сохраняет свойства непрерывности, поскольку амплитуды uд(iTд) могут принимать произвольные значения. Такая форма преобразования аналогового сигнала называется дискретизацией по времени, а время Тд – периодом дискретизации.
Если в качестве дискретных выбрать m уровней напряжений, то функция uа(t) вырождается в ступенчатую функцию uк(jQ), где j=1,m, в которой каждый следующий потенциал отличается от предыдущего на одинаковую величину Q, называемую квантом (рис. 10.1,б). Поскольку функция uа(t) может иметь произвольную, необязательно линейную форму, то очевидно, что пересечения этой функции с квантованными уровнями jQ будут наблюдаться в неравные промежутки времени Dti=ti-ti-1. При этом значения функций uа(ti) и uк(jQ) в моменты времени ti будут совпадать, а сами моменты времени ti могут быть произвольными и определяться формой uа(t) и выбранными уровнями jQ. Отсюда следует, что ступенчатая функция uк(jQ) сохраняет свойство непрерывности по времени. Такое преобразование аналогового сигнала носит название квантование по уровню.
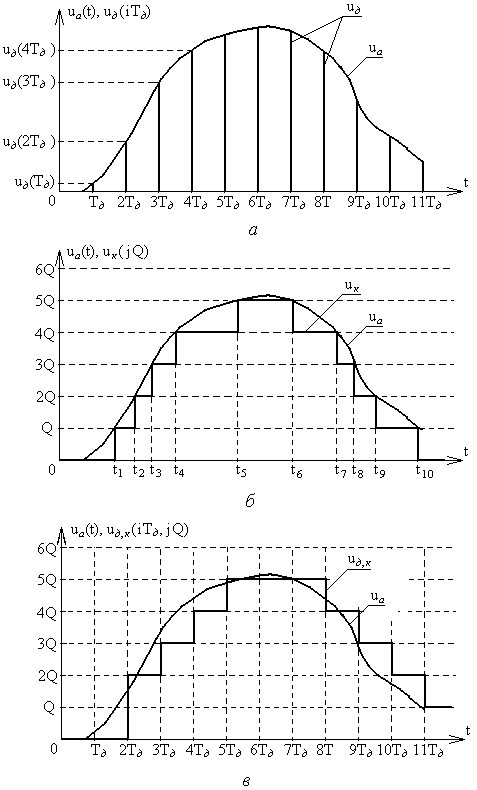
Рис. 10.1. Дискретизация аналогового сигнала по времени (а), квантование по уровню (б), дискретизация и квантование по времени и уровню (в).
Для того, чтобы проведенное преобразование стало аналого-цифровым, в соответствие значению каждого уровня jQ необходимо присвоить цифровой код Xj, в большинстве случаев двоичный. Такой процесс называется кодированием. Обычно цифровой код выбирается равным десятичному эквиваленту номера j квантованного уровня. В этом случае максимальному значению кода соответствует значение максимально возможного входного напряжения АЦП за вычетом одного кванта uвх.max-Q. Объясняется это тем, что одна кодовая комбинация соответствует нулевому значению входного напряжения АЦП. Рассмотрим основные характеристики устройств аналого-цифрового преобразования.
Разрядность n выходного кода для АЦП и входного для ЦАП – характеризует количество разрядов для отображения аналоговой преобразуемой величины. Эта характеристика определяет количество квантованных уровней m=2n.
Диапазон входного Uвх. или выходного Uвых. напряжений АЦП или ЦАП соответственно - характеризует полный диапазон входного (выходного) напряжения, которое преобразователь в состоянии отобразить принятым выходным (входным) кодом. Выражается в единицах Вольт. Диапазон данного напряжения может быть как однополярным, так и биполярным в зависимости от типа преобразователя.
Разрешающая способность (чувствительность) – значение минимального изменения входного сигнала АЦП, которое вызывает изменение цифрового кода на единицу. Эта характеристика определяется величиной кванта Q и называется еще величиной младшего разряда (МЗР или LSB в англоязычной терминологии). Из-за наличия неопределенности (погрешности) величиной ±Q/2 обычно принимается, что изменение цифрового кода на единицу происходит в средней точке диапазона данного квантованного уровня (рис. 10.2,а). Аналогично для ЦАП разрешающая способность – это минимальное изменение выходного аналогового сигнала, обусловленное изменением входного цифрового кода на единицу.
Напряжение смещения нуля Uсм.0 – напряжение на входе АЦП, при котором на выходе устанавливается нулевой код. Величина Uсм0 определяется сдвигом реальной uр от идеальной uид передаточных характеристик (рис. 10.2,б). Соответственно для ЦАП напряжение смещения нуля – это величина выходного напряжения при нулевом входном коде. Напряжение смещения нуля характеризует аддитивную погрешность преобразователя. Часто Uсм.0 выражается в единицах МЗР.
Абсолютная погрешность преобразования в конечной точке шкалы dUf - характеризует отклонение реального максимального входного напряжения для АЦП или выходного для ЦАП от идеального значения, определенного технической документацией преобразователя (рис. 10.2,в). Данная величина определяет угол наклона реальной передаточной характеристики и мультипликативную погрешность преобразователя. Также как и Uсм.0 часто выражается в единицах МЗР.
Интегральная нелинейность dUL - характеризует максимально возможное отклонение реальной передаточной характеристики АЦП (ЦАП) от заданной идеальной при нулевых значениях Uсм.0 и dUf (рис. 10.2,г). Выражается в единицах МЗР или в процентах по отношению к максимальному входному (выходному) напряжению преобразователя.
Дифференциальная нелинейность dUдиф. - характеризует максимальное отклонение величины одного из квантов АЦП (ЦАП) от идеального аналогового значения Q (рис. 10.2,д). Выражается в единицах МЗР или в процентах по отношению к максимальному входному (выходному) напряжению. Если дифференциальная нелинейность АЦП превышает 1 МЗР, то в выходном коде могут выпадать одна или несколько кодовых комбинаций Хвып. Аналогично если дифференциальная нелинейность ЦАП превышает 1 МЗР, то в выходном напряжении могут выпадать один или несколько квантованных уровней.
Время преобразования tс для АЦП - характеризует временной интервал с момента подачи управляющего сигнала «начало преобразования» и до момента получения на выходе адекватного цифрового кода. Изменение входного аналогового сигнала в период времени tc нежелательно, поскольку это изменение вносит неопределенность в генерируемый выходной код. Для ЦАП аналогичный параметр носит название времени установления ts выходного аналогового сигнала. Очевидно, что входной цифровой код в данный период времени должен оставаться неизменным.
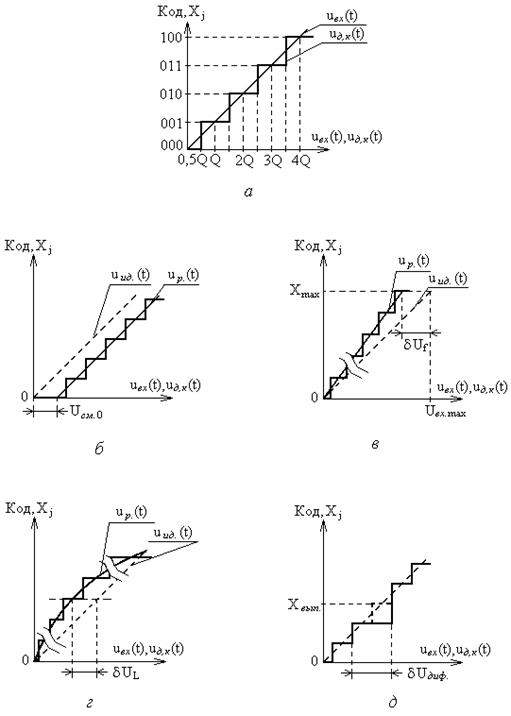
Рис. 10.2. Пояснения к характеристикам АЦП: (а) - разрешающая способность Q, (б) - напряжение смещения нуля Uсм.0, (в) - абсолютная погрешность преобразования в конечной точке шкалы dUf, (г) - итегральная нелинейность dUL, (д) - дифференциальная нелинейность dUдиф.
Максимальная частота преобразования fс.max - определяет максимальное значение числа отсчетов входного сигнала, выполняемых преобразователем в единицу времени при сохранении полной точности. Если входной аналоговый сигнал АЦП можно представить в виде конечной суммы гармонических составляющих, т.е. конечным частотным спектром 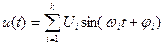 , то выбор fc определяется теоремой Котельникова. Согласно этой теореме частоту преобразования АЦП следует выбирать большей или равной удвоенной частоте fk максимальной гармоники входного аналогового сигнала:
, то выбор fc определяется теоремой Котельникова. Согласно этой теореме частоту преобразования АЦП следует выбирать большей или равной удвоенной частоте fk максимальной гармоники входного аналогового сигнала:
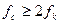 ,
,
где 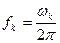 .
.
Дата добавления: 2022-02-05; просмотров: 800;











