Квантование измерительных сигналов

Преобразование непрерывного сигнала в дискретный, состоящий из множества квантов, называется квантованием по уровню (рис. 4.5).

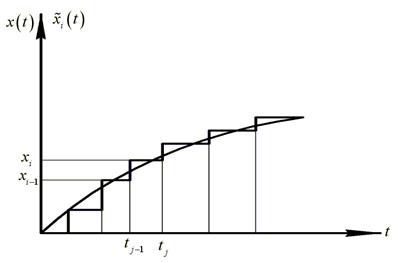
Рис. 4.5. Квантование сигнала по уровню

При квантовании по уровню диапазон возможных измерений (0, T) сигнала x(t) разбивается на n одинаковых или разных по величине интервалов квантования

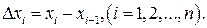
При квантовании любое значение 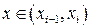округляется до некоторой величины 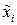, называемой уровнем квантования.

Уровень квантования 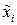как функцию времени можно представить в виде произведения единичной функции

,

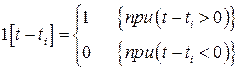умноженной на масштаб 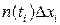, т. е.

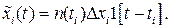(4.33)

При замене истинных значений функции x(t) квантованными значениями 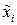возникает погрешность

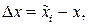(4.34)

которая определяется свойствами сигнала и характером (равномерное или неравномерное квантование) квантования.

Для равномерного квантования по уровню 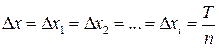и наибольшая погрешность

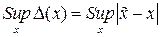
будет минимальна при заданном n квантов, если 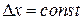и и 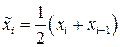определяется соотношением

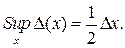(4.35)

То есть наибольшая погрешность не превышает половины интервала квантования. Для уменьшения погрешности квантования необходимо уменьшать интервал квантования.

Поскольку погрешность квантования является случайной, то следует оценить ее статические характеристики.

Математическое ожидание

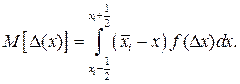(4.36)

Дисперсия

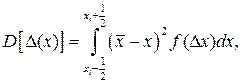(4.37)

где 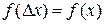плотность распределения погрешности, принимаемой такой же, как и сигнала x(t).

Для большого числа квантов n плотность вероятности f(x) внутри ступени квантования практически постоянна и ее можно вынести за знаки интегралов.

Если вычисление математического ожидания показывает, что 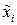соответствует середине интервала квантования, то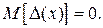

Для дисперсии, можно получить соотношение

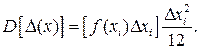(4.38)

Если учесть изменение сигнала во всем диапазоне (0, T), то для дисперсии можно записать

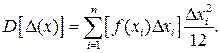(4.39)

Если выполняется условие нормирования

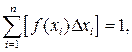(4.40)

то выражение для дисперсии погрешности квантования принимает вид

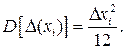(4.41)

Среднеквадратическое значение погрешности квантования

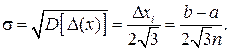(4.42)

Отсюда при заданной погрешности σ можно определить число ступеней n квантования

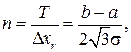(4.43)

где a и b – верхнее и нижнее значения квантуемого сигнала x(t).

Полученные соотношения справедливы для равномерного квантования. Исследования показывают, что с точки зрения уменьшения среднеквадратической погрешности более выгодно неравномерное квантование, хотя техническая реализация его более сложна.