Квантование в поликремниевом затворе

Квантование инверсного слоя происходит вследствие того, что электроны находятся в потенциальной яме, размеры которой сравнимы с длиной волны электрона. Однако квантовые эффекты проявляются не только в режиме инверсии, но также в режимах обогащения, обеднения и даже в режиме плоских зон. В режиме обогащения изгиб зон в кремнии составляет самое большее несколько десятков милливольт, в то время как в режиме обеднения носители удаляются от границы окисел-кремний и формируется глубокая потенциальная яма. Однако, как при обогащении, так и при обеднении носители находятся от границы окисел-кремний на расстоянии, сравнимом с длиной волны электрона, так что необходимо принимать во внимание квантовомеханические эффекты. Это является следствием присутствия высокого (практически бесконечно высокого) потенциального барьера на границе окисел-кремний. На этой границе волновая функция, а вместе с ней и плотность электронного газа, должны обращаться в нуль. В присутствии резкого потенциального барьера происходит интерференция волновых функций основных носителей (электронов), и квантовомеханический заряд отталкивается от поверхности. Создается так называемое «темное пространство», в котором концентрация основных носителей уменьшается по сравнению с концентрацией примеси. В режиме плоских зон протяженность темного пространства составляет примерно [4]

,

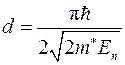где − типичная энергия носителей заряда выше дна зоны проводимости. Для невырожденного электронного газа величина , а для вырожденного 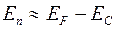. В кремнии величина 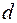для электронов и дырок составляет 2-3нм. Поскольку темное пространство есть прямое следствие резкого потенциального барьера, в поликремниевом затворе имеются необходимые условия его появления.

На рис.9.9 представлены зависимости концентрации электронов от расстояния от границы поликремний/окисел в п+-поликремнии МОП-структуры с толщиной окисла 5нм, полученные для классического случая и для самосогласованного решения уравнений Шредингера-Пуассона [4]. Результаты представлены для режима обогащения ( 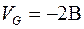), при пороге ( 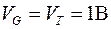) и при сильной инверсии ( ). Заметим, что при положительном напряжении на затворе подложка и затвор обеднены, в то время как при отрицательном напряжении –

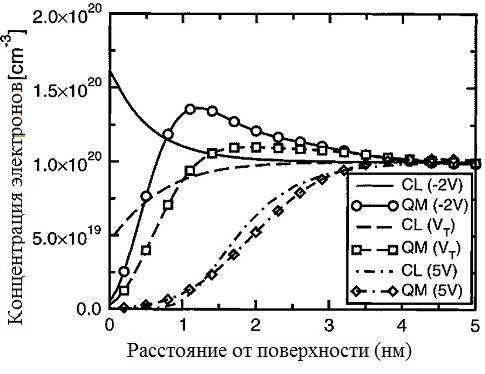
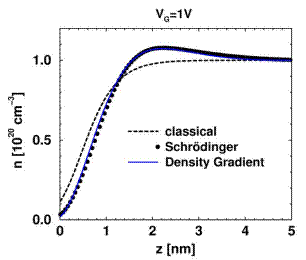
Рис.9.9. Распределение концентрации электронов в поликремния п-типа в пМОПТ с толщиной окисла 5нм. Поликремний легирован до 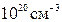. Результаты приведены для классической (CL) и квантовомеханической (QM) моделей при различных режимах смещения затвора: в обогащении (-2В), при пороговом напряжении 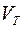=1В и при 5В. [4].

обогащены. Видна значительная разница между классическим и КМ распределениями зарядов, где классическое распределение имеет максимум на границе раздела в режиме обогащения. Значительная разница видна даже в режиме обеднения поликремния. Фактически, пока толщина слоя (классического) обеднения поликремния сравнима или меньше размеров темного пространства, обедненный слой будет определяться КМ-эффектом и будет больше классической величины. Это КМ расширение обедненного слоя можно видеть в распределении концентрации при пороговом напряжении на рис.9.9. Заметим, что при указанной высокой концентрации примеси в затворе концентрация электронов на границе раздела лишь слегка уменьшается при пороговом напряжении в классическом случае, но значительно модифицируется при КМ рассмотрении.

Расчеты показывают, что при легировании поликремния выше 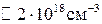толщина слоя обеднения становится меньше протяженности темного пространства, КМ эффекты становятся важными также и при сильной инверсии.

Влияние на пороговое напряжение. Как видно из рис.9.9, при всех условиях смещения, за исключением обогащения, существует минимальная область обеднения, порядка 1нм, где концентрация основных носителей заряда меньше, чем концентрация активной примеси. Для п+-поликремния с концентрацией примеси 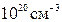это соответствует существованию поверхностного фиксированного положительного заряда величиной примерно . При пороге зарядом электронов в канале можно пренебречь, в то время как общий отрицательный заряд обеднения (ионов) в подложке типично составляет порядка нескольких 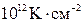. Для достижения электронейтральности всей системы необходим избыточный заряд электронов в поликремнии, чтобы обеспечить необходимый отрицательный компенсирующий заряд. Это распределение, обозначенное как «QM (V_T)» на рис.9.9, демонстрирует выпуклость в распределении электронов на глубине примерно 2нм. Присутствие двух реально существующих зарядовых плоскостей, одной положительной и одной отрицательной, разделенных расстоянием примерно 1нм, создает электрический диполь (рис.9.10). На области, заключенной между этими двумя плоскостями, падает конечное напряжение, которое проявляется как сдвиг порогового напряжения на величину порядка нескольких десятков милливольт.

Рис.9.10.Формирование «квантового диполя» в поликремнии. Квантовое обеднение поликремния уменьшается при увеличении напряжения на затворе [5].

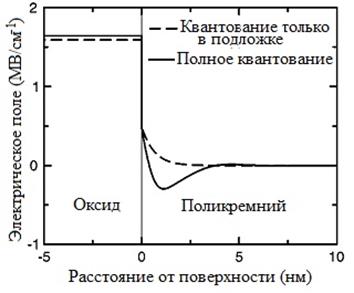
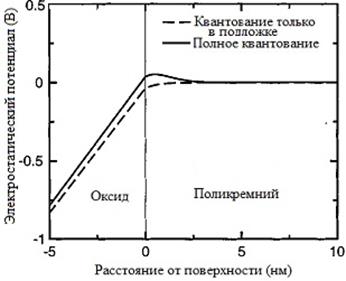
Рис.9.11. Электрическое поле (а) и электростатический потенциал (б) при пороге в окисле и поликремнии в модели квантования только в подложке (пунктир) и полной квантовой модели – в подложке и поликремнии – (сплошная линия). Параметры прибора те же, что и на рис.9.9. [4].

Влияние зарядового диполя на электрическое поле и электростатический потенциал иллюстрирует рис.9.11. В то время как при классическом решении электрическое поле в поликремнии плавно увеличивается по направлению к границе раздела окисел/поликремний (не показано на рис.), квантовое решение предсказывает сначала отрицательный пик вследствие избытка электронов, и потом быстрый подъем к положительному значению на границе, соответствующему заряду области обеднения внутри области темного пространства. Отрицательный пик электрического поля в поликремнии приводит к увеличению поля в окисле, так как полное падение напряжения между электронейтральной областью поликремния и объемом кремния то же самое для обоих случаев. Увеличение поля в окисле означает, что больший инверсный заряд накапливается на стороне подложки для данного смещения затвора. Следовательно, квантование в поликремнии определяет отрицательный сдвиг порогового напряжения (уменьшает V_T), что противоположно квантованию носителей в канале, которое вызывает положительный сдвиг (увеличивает V_T).

Рис.9.12. Сдвиг порогового напряжения вследствие квантовомеханических эффектов в зависимости от толщины окисла. Результаты показаны для случая квантования только в подложке (QMS) и для полного квантования (FQ) [4].

Из проведенного рассмотрения можно ожидать, что интенсивность диполя и величина сдвига порога сильно зависят от уровня легирования поликремния. Рис.9.12 показывает смоделированный сдвиг порогового напряжения относительно чисто классической модели, представленный в зависимости от толщины окисла. Результаты представлены для концентрации в подложке и уровня легирования поликремния от 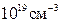до 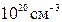. Если принимается во внимание только квантование в подложке, положительный сдвиг порогового напряжения составляет примерно от 75мВ до 125мВ, который слабо зависит от легирования поликремния в результате малого падения напряжения на нем (см. QMS на рис.9.12). Наоборот, учет квантования на границе раздела поликремний/окисел приводит к отрицательному сдвигу, который сильно зависит от легирования поликремния. Для отрицательный сдвиг напряжения составляет примерно 80мВ, значительно отличаясь от традиционного результата, полученного при классическом моделировании поликремния. Кроме того, обращает внимание, что сдвиг порогового напряжения вследствие квантования в поликремнии не зависит от рассмотрения (классического или КМ), принятого для подложки. Это объясняет, почему традиционное исследование КМ эффектов в МОПТ не обнаруживает такого отрицательного сдвига. Заметим также, что квантование поликремния приводит к сдвигу порогового напряжения, который не зависит от толщины окисла, поскольку зарядовый диполь локализован внутри поликремния затвора.

Легко видеть, что все кривые зависимости сдвига порога от толщины окисла (рис.9.12) параллельны друг другу, то есть характер нарастания определяется одной и той же причиной и при классическом и при квантовом рассмотрении. Этой причиной является падение напряжения на окисле при увеличении его толщины. Действительно, например, в классическом случае при пороге

, (9.7.1)

где 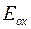, − электрическое поле в окисле и полупроводнике. При увеличении толщины окисла в выражении (9.7.1) изменяется только последний член, определяя линейную зависимость от толщины окисла. При квантовом рассмотрении в выражении (9.7.1) изменяется на 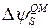только величина изгиба зон и электрическое поле в полупроводнике, характер же зависимости сохраняется.