Энтропия сложного события, состоящего из нескольких зависимых событий

Теперь предположим, что элементы сообщения (буквы) взаимозависимы. В этом случае вероятность появления последовательности из нескольких букв не равна произведению вероятностей появления каждой из этих букв в отдельности. Так, если, к примеру, сообщение состоит из двух букв a и b, то .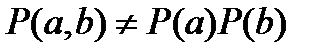

Как и в предыдущий раз, предположим, имеется сообщение, состоящее из n букв: 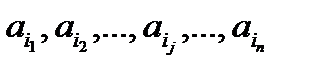, где j=1, 2, …, n – номера букв в сообщении по порядку, а i₁, i₂, … ,i_n номера букв из алфавита.

С учетом взаимозависимости между буквами вероятность его получения теперь находится через произведение условных вероятностей:

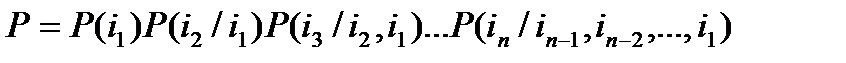(3)

Заметим, что эти условные вероятности можно найти, используя взаимные вероятности по следующим формулам:

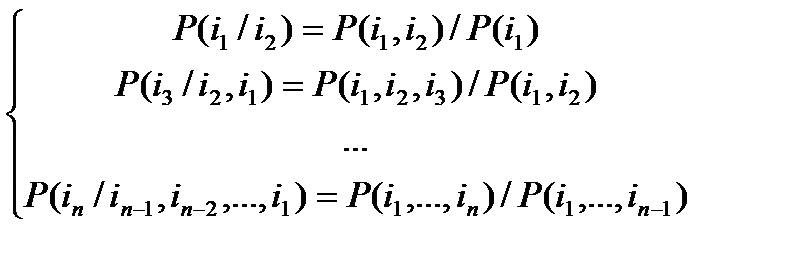(4)

Подставив (4) в (3), получим:

.

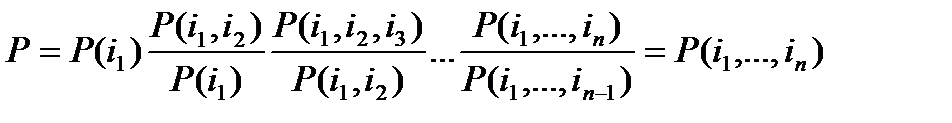После сокращения одинаковых членов в числителе и знаменателе получаем: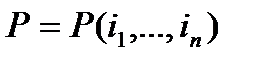

Возможны различные варианты зависимостей между буквами сообщения. Предположим, что эта зависимость распространяется только на s рядом расположенных букв.

Для вывода общей формулы среднего значения энтропии на одну букву сообщения со взаимозависимыми рядом стоящими буквами начнем с ограниченного примера. Положим, что эта зависимость распространяется только на 3 буквы, а сообщение состоит всего из 6 букв. Тогда:

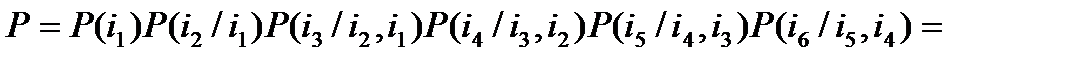
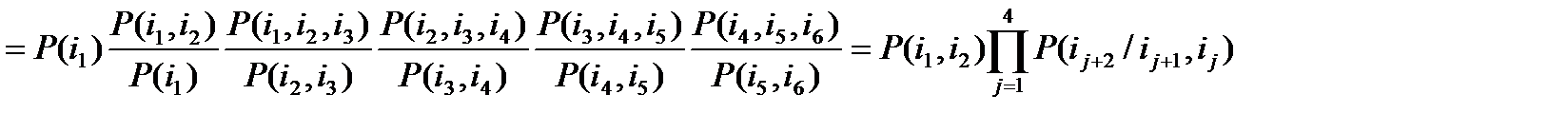
Найдем теперь энтропию этого сообщения:

.

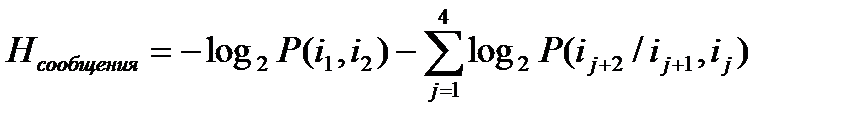Найдем теперь среднее значение энтропии на одну букву сообщения. Для этого нужно найти предел, к которому стремится частное от деления энтропии сообщения на его длину при увеличении длины до бесконечности:

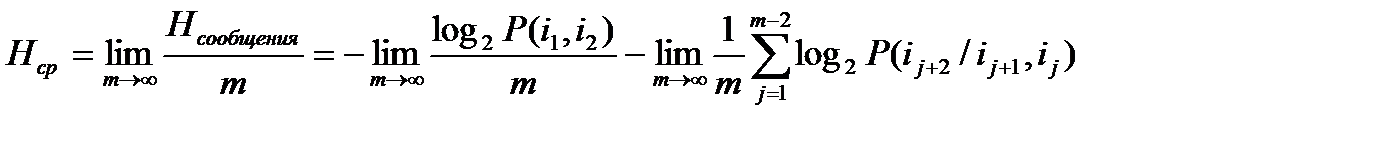. (5)

Первое слагаемое в (5) в пределе равно 0. Второе слагаемое можно разложить на ряд сумм, члены которых являются взаимными вероятностями одних и тех же комбинаций букв. Обозначим количество этих комбинаций N_ijk. С учетом этого и обозначая объем алфавита буквой r (5) преобразуется к виду:

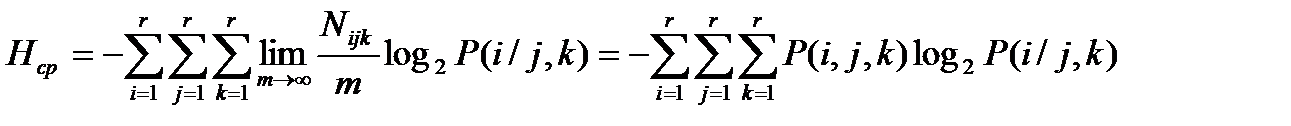
Аналогичным образом легко получить формулу для случая, когда зависимость распространяется на 2 соседние буквы:

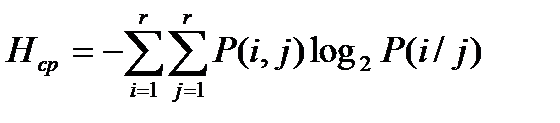
и на произвольное число S соседних букв:

.

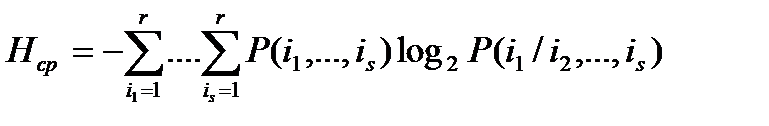Учтем при этом, что:

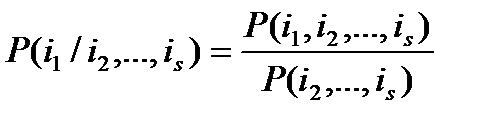и .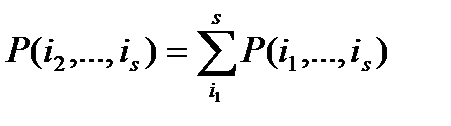

Таким образом, для вычисления энтропии в этом случае достаточно знать только матрицу взаимных вероятностей P(i₁,…,i_s).

Если же события, из которых состоит сложное событие, не являются независимыми, вероятность этого сложного события не равна произведению вероятностей событий, его составляющих: .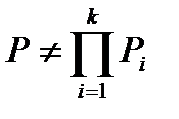

Зная характер зависимости между составляющими сложного сообщения можно, уменьшить неопределенность (энтропию) этого сложного сообщения. Для этого нужно знать набор взаимных вероятностей. Так например, если сложным сообщением считать текст, состоящий из взаимозависимых букв и если зависимость между буквами распространяется на n рядом стоящих в сообщении букв, то для учета связей между этими буквами нужно знать матрицу взаимных вероятностей P(i₁, i₂, …, i_n,) , где 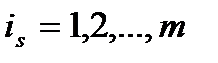─ буквы из алфавита объемом m.

Энтропия сообщения, состоящего из n таких букв, подсчитывается согласно определению .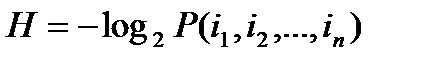

Средняя энтропия такого сообщения:

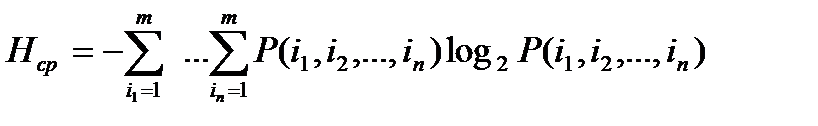, где m – объем алфавита.

Среднее количество информации, приходящееся на букву такого сообщения: .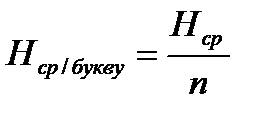

Пример:

Возьмем текстовый файл. Известно, что в нем используется всего 256 символов. Таким образом, объем алфавита m = 256.

Если текст состоит из независимых букв, то для определения его энтропии достаточно знать всего 256 вероятностей P_i , 0<=i<=255.

Если же зависимость распространяется на 2 рядом стоящие буквы, что вообще-то не так, то матрица вероятностей 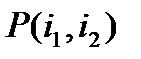будет уже иметь в своем составе 256•256 = 2¹⁶ = 65536 элементов.

Распространение зависимости на 3 и более букв увеличивает размер матрицы в геометрической прогрессии.